Skip to contents

Update an existing mvgam object

Source: R/update.mvgam.R
update.mvgam.Rd

This function allows a previously fitted mvgam model to be updated

Usage

# S3 method for mvgam
update(
  object,
  formula,
  trend_formula,
  knots,
  trend_knots,
  trend_model,
  family,
  share_obs_params,
  data,
  newdata,
  trend_map,
  use_lv,
  n_lv,
  priors,
  chains,
  burnin,
  samples,
  threads,
  algorithm,
  lfo = FALSE,
  ...
)

# S3 method for jsdgam
update(
  object,
  formula,
  factor_formula,
  knots,
  factor_knots,
  data,
  newdata,
  n_lv,
  family,
  share_obs_params,
  priors,
  chains,
  burnin,
  samples,
  threads,
  algorithm,
  lfo = FALSE,
  ...
)

Arguments

object

list object returned from mvgam. See mvgam()

formula

Optional new formula object. Note, mvgam currently does not support dynamic formula updates such as removal of specific terms with - term. When updating, the entire formula needs to be supplied

trend_formula

An optional formula object specifying the GAM process model formula. If supplied, a linear predictor will be modelled for the latent trends to capture process model evolution separately from the observation model. Should not have a response variable specified on the left-hand side of the formula (i.e. a valid option would be ~ season + s(year)). Also note that you should not use the identifier series in this formula to specify effects that vary across time series. Instead you should use trend. This will ensure that models in which a trend_map is supplied will still work consistently (i.e. by allowing effects to vary across process models, even when some time series share the same underlying process model). This feature is only currently available for RW(), AR() and VAR() trend models. In nmix() family models, the trend_formula is used to set up a linear predictor for the underlying latent abundance. Be aware that it can be very challenging to simultaneously estimate intercept parameters for both the observation mode (captured by formula) and the process model (captured by trend_formula). Users are recommended to drop one of these using the - 1 convention in the formula right hand side.

knots

An optional list containing user specified knot values to be used for basis construction. For most bases the user simply supplies the knots to be used, which must match up with the k value supplied (note that the number of knots is not always just k). Different terms can use different numbers of knots, unless they share a covariate

trend_knots

As for knots above, this is an optional list of knot values for smooth functions within the trend_formula

trend_model

character or function specifying the time series dynamics for the latent trend. Options are:

  • None (no latent trend component; i.e. the GAM component is all that contributes to the linear predictor, and the observation process is the only source of error; similarly to what is estimated by gam)

  • ZMVN or ZMVN() (Zero-Mean Multivariate Normal; only available in Stan)

  • 'RW' or RW()

  • 'AR1' or AR(p = 1)

  • 'AR2' or AR(p = 2)

  • 'AR3' or AR(p = 3)

  • 'CAR1' or CAR(p = 1)

  • 'VAR1' or VAR()(only available in Stan)

  • 'PWlogistic, 'PWlinear' or PW() (only available in Stan)

  • 'GP' or GP() (Gaussian Process with squared exponential kernel; only available in Stan)

For all trend types apart from ZMVN(), GP(), CAR() and PW(), moving average and/or correlated process error terms can also be estimated (for example, RW(cor = TRUE) will set up a multivariate Random Walk if n_series > 1). It is also possible for many multivariate trends to estimate hierarchical correlations if the data are structured among levels of a relevant grouping factor. See mvgam_trends for more details and see ZMVN for an example.

family

family specifying the exponential observation family for the series. Currently supported families are:

  • gaussian() for real-valued data

  • betar() for proportional data on (0,1)

  • lognormal() for non-negative real-valued data

  • student_t() for real-valued data

  • Gamma() for non-negative real-valued data

  • bernoulli() for binary data

  • poisson() for count data

  • nb() for overdispersed count data

  • binomial() for count data with imperfect detection when the number of trials is known; note that the cbind() function must be used to bind the discrete observations and the discrete number of trials

  • beta_binomial() as for binomial() but allows for overdispersion

  • nmix() for count data with imperfect detection when the number of trials is unknown and should be modeled via a State-Space N-Mixture model. The latent states are Poisson, capturing the 'true' latent abundance, while the observation process is Binomial to account for imperfect detection. See mvgam_families for an example of how to use this family

Default is poisson(). See mvgam_families for more details

share_obs_params

logical. If TRUE and the family has additional family-specific observation parameters (e.g. variance components in student_t() or gaussian(), or dispersion parameters in nb() or betar()), these parameters will be shared across all outcome variables. This is handy if you have multiple outcomes (time series in most mvgam models) that you believe share some properties, such as being from the same species over different spatial units. Default is FALSE.

data

A dataframe or list containing the model response variable and covariates required by the GAM formula and optional trend_formula. Most models should include columns:

  • series (a factor index of the series IDs; the number of levels should be identical to the number of unique series labels (i.e. n_series = length(levels(data$series))))

  • time (numeric or integer index of the time point for each observation). For most dynamic trend types available in mvgam (see argument trend_model), time should be measured in discrete, regularly spaced intervals (i.e. c(1, 2, 3, ...)). However you can use irregularly spaced intervals if using trend_model = CAR(1), though note that any temporal intervals that are exactly 0 will be adjusted to a very small number (1e-12) to prevent sampling errors. See an example of CAR() trends in CAR

Note however that there are special cases where these identifiers are not needed. For example, models with hierarchical temporal correlation processes (e.g. AR(gr = region, subgr = species)) should NOT include a series identifier, as this will be constructed internally (see mvgam_trends and AR for details). mvgam can also fit models that do not include a time variable if there are no temporal dynamic structures included (i.e. trend_model = 'None' or trend_model = ZMVN()). data should also include any other variables to be included in the linear predictor of formula

newdata

Optional dataframe or list of test data containing the same variables as in data. If included, the observations in variable y will be set to NA when fitting the model so that posterior simulations can be obtained

trend_map

Optional data.frame specifying which series should depend on which latent trends. Useful for allowing multiple series to depend on the same latent trend process, but with different observation processes. If supplied, a latent factor model is set up by setting use_lv = TRUE and using the mapping to set up the shared trends. Needs to have column names series and trend, with integer values in the trend column to state which trend each series should depend on. The series column should have a single unique entry for each series in the data (names should perfectly match factor levels of the series variable in data). Note that if this is supplied, the intercept parameter in the process model will NOT be automatically suppressed. See examples for details

use_lv

logical. If TRUE, use dynamic factors to estimate series' latent trends in a reduced dimension format. Only available for RW(), AR() and GP() trend models. Defaults to FALSE

n_lv

integer the number of latent dynamic factors to use if use_lv == TRUE. Cannot be > n_series. Defaults arbitrarily to min(2, floor(n_series / 2))

priors

An optional data.frame with prior definitions or, preferentially, a vector containing objects of class brmsprior (see. prior for details). See get_mvgam_priors and Details' for more information on changing default prior distributions

chains

integer specifying the number of parallel chains for the model. Ignored if algorithm %in% c('meanfield', 'fullrank', 'pathfinder', 'laplace')

burnin

integer specifying the number of warmup iterations of the Markov chain to run to tune sampling algorithms. Ignored if algorithm %in% c('meanfield', 'fullrank', 'pathfinder', 'laplace')

samples

integer specifying the number of post-warmup iterations of the Markov chain to run for sampling the posterior distribution

threads

integer Experimental option to use multithreading for within-chain parallelisation in Stan. We recommend its use only if you are experienced with Stan's reduce_sum function and have a slow running model that cannot be sped up by any other means. Currently works for all families apart from nmix() and when using Cmdstan as the backend

algorithm

Character string naming the estimation approach to use. Options are "sampling" for MCMC (the default), "meanfield" for variational inference with factorized normal distributions, "fullrank" for variational inference with a multivariate normal distribution, "laplace" for a Laplace approximation (only available when using cmdstanr as the backend) or "pathfinder" for the pathfinder algorithm (only currently available when using cmdstanr as the backend). Can be set globally for the current R session via the "brms.algorithm" option (see options). Limited testing suggests that "meanfield" performs best out of the non-MCMC approximations for dynamic GAMs, possibly because of the difficulties estimating covariances among the many spline parameters and latent trend parameters. But rigorous testing has not been carried out

lfo

Logical indicating whether this is part of a call to lfo_cv.mvgam. Returns a lighter version of the model with no residuals and fewer monitored parameters to speed up post-processing. But other downstream functions will not work properly, so users should always leave this set as FALSE

...

Other arguments to be passed to mvgam or jsdgam

factor_formula

Optional new formula object for the factor linear predictors

factor_knots

An optional list containing user specified knot values to be used for basis construction of any smooth terms in factor_formula. For most bases the user simply supplies the knots to be used, which must match up with the k value supplied (note that the number of knots is not always just k). Different terms can use different numbers of knots, unless they share a covariate

Value

A list object of class mvgam containing model output, the text representation of the model file, the mgcv model output (for easily generating simulations at unsampled covariate values), Dunn-Smyth residuals for each outcome variable and key information needed for other functions in the package. See mvgam-class for details. Use methods(class = "mvgam") for an overview on available methods.

A list object of class mvgam containing model output, the text representation of the model file, the mgcv model output (for easily generating simulations at unsampled covariate values), Dunn-Smyth residuals for each series and key information needed for other functions in the package. See mvgam-class for details. Use methods(class = "mvgam") for an overview on available methods.

Author

Nicholas J Clark

Examples

# \donttest{
# Simulate some data and fit a Poisson AR1 model
simdat <- sim_mvgam(n_series = 1, trend_model = AR())
mod <- mvgam(y ~ s(season, bs = 'cc'),
             trend_model = AR(),
             noncentred = TRUE,
             data = simdat$data_train,
             chains = 2)
#> Compiling Stan program using cmdstanr
#> 
#> Start sampling
#> Running MCMC with 2 parallel chains...
#> 
#> Chain 1 Iteration:   1 / 1000 [  0%]  (Warmup) 
#> Chain 1 Iteration: 100 / 1000 [ 10%]  (Warmup) 
#> Chain 1 Iteration: 200 / 1000 [ 20%]  (Warmup) 
#> Chain 2 Iteration:   1 / 1000 [  0%]  (Warmup) 
#> Chain 1 Iteration: 300 / 1000 [ 30%]  (Warmup) 
#> Chain 1 Iteration: 400 / 1000 [ 40%]  (Warmup) 
#> Chain 1 Iteration: 500 / 1000 [ 50%]  (Warmup) 
#> Chain 1 Iteration: 501 / 1000 [ 50%]  (Sampling) 
#> Chain 2 Iteration: 100 / 1000 [ 10%]  (Warmup) 
#> Chain 2 Iteration: 200 / 1000 [ 20%]  (Warmup) 
#> Chain 1 Iteration: 600 / 1000 [ 60%]  (Sampling) 
#> Chain 2 Iteration: 300 / 1000 [ 30%]  (Warmup) 
#> Chain 2 Iteration: 400 / 1000 [ 40%]  (Warmup) 
#> Chain 1 Iteration: 700 / 1000 [ 70%]  (Sampling) 
#> Chain 2 Iteration: 500 / 1000 [ 50%]  (Warmup) 
#> Chain 2 Iteration: 501 / 1000 [ 50%]  (Sampling) 
#> Chain 1 Iteration: 800 / 1000 [ 80%]  (Sampling) 
#> Chain 2 Iteration: 600 / 1000 [ 60%]  (Sampling) 
#> Chain 1 Iteration: 900 / 1000 [ 90%]  (Sampling) 
#> Chain 1 Iteration: 1000 / 1000 [100%]  (Sampling) 
#> Chain 2 Iteration: 700 / 1000 [ 70%]  (Sampling) 
#> Chain 1 finished in 0.9 seconds.
#> Chain 2 Iteration: 800 / 1000 [ 80%]  (Sampling) 
#> Chain 2 Iteration: 900 / 1000 [ 90%]  (Sampling) 
#> Chain 2 Iteration: 1000 / 1000 [100%]  (Sampling) 
#> Chain 2 finished in 1.2 seconds.
#> 
#> Both chains finished successfully.
#> Mean chain execution time: 1.1 seconds.
#> Total execution time: 1.6 seconds.
#> 
summary(mod)
#> GAM formula:
#> y ~ s(season, bs = "cc")
#> <environment: 0x0000024db9be6178>
#> 
#> Family:
#> poisson
#> 
#> Link function:
#> log
#> 
#> Trend model:
#> AR()
#> 
#> 
#> N series:
#> 1 
#> 
#> N timepoints:
#> 75 
#> 
#> Status:
#> Fitted using Stan 
#> 2 chains, each with iter = 1000; warmup = 500; thin = 1 
#> Total post-warmup draws = 1000
#> 
#> 
#> GAM coefficient (beta) estimates:
#>              2.5%    50%  97.5% Rhat n_eff
#> (Intercept) -0.75 -0.390 -0.065 1.01   629
#> s(season).1  0.24  0.700  1.200 1.00   628
#> s(season).2 -0.63  0.058  0.590 1.00   707
#> s(season).3 -1.00 -0.310  0.210 1.00   714
#> s(season).4 -0.98 -0.350  0.260 1.00   849
#> s(season).5 -1.10 -0.400  0.220 1.00   791
#> s(season).6 -1.30 -0.680 -0.048 1.00   871
#> s(season).7 -1.40 -0.690 -0.100 1.00   676
#> s(season).8 -1.00 -0.350  0.210 1.00   701
#> 
#> Approximate significance of GAM smooths:
#>           edf Ref.df Chi.sq p-value  
#> s(season) 3.6      8   19.2   0.061 .
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Latent trend parameter AR estimates:
#>            2.5%   50% 97.5% Rhat n_eff
#> ar1[1]   -0.970 -0.52  0.53 1.00   423
#> sigma[1]  0.084  0.53  0.94 1.03   171
#> 
#> Stan MCMC diagnostics:
#> n_eff / iter looks reasonable for all parameters
#> Rhat looks reasonable for all parameters
#> 0 of 1000 iterations ended with a divergence (0%)
#> 0 of 1000 iterations saturated the maximum tree depth of 10 (0%)
#> E-FMI indicated no pathological behavior
#> 
#> Samples were drawn using NUTS(diag_e) at Mon Nov 18 10:36:57 AM 2024.
#> For each parameter, n_eff is a crude measure of effective sample size,
#> and Rhat is the potential scale reduction factor on split MCMC chains
#> (at convergence, Rhat = 1)
conditional_effects(mod, type = 'link')


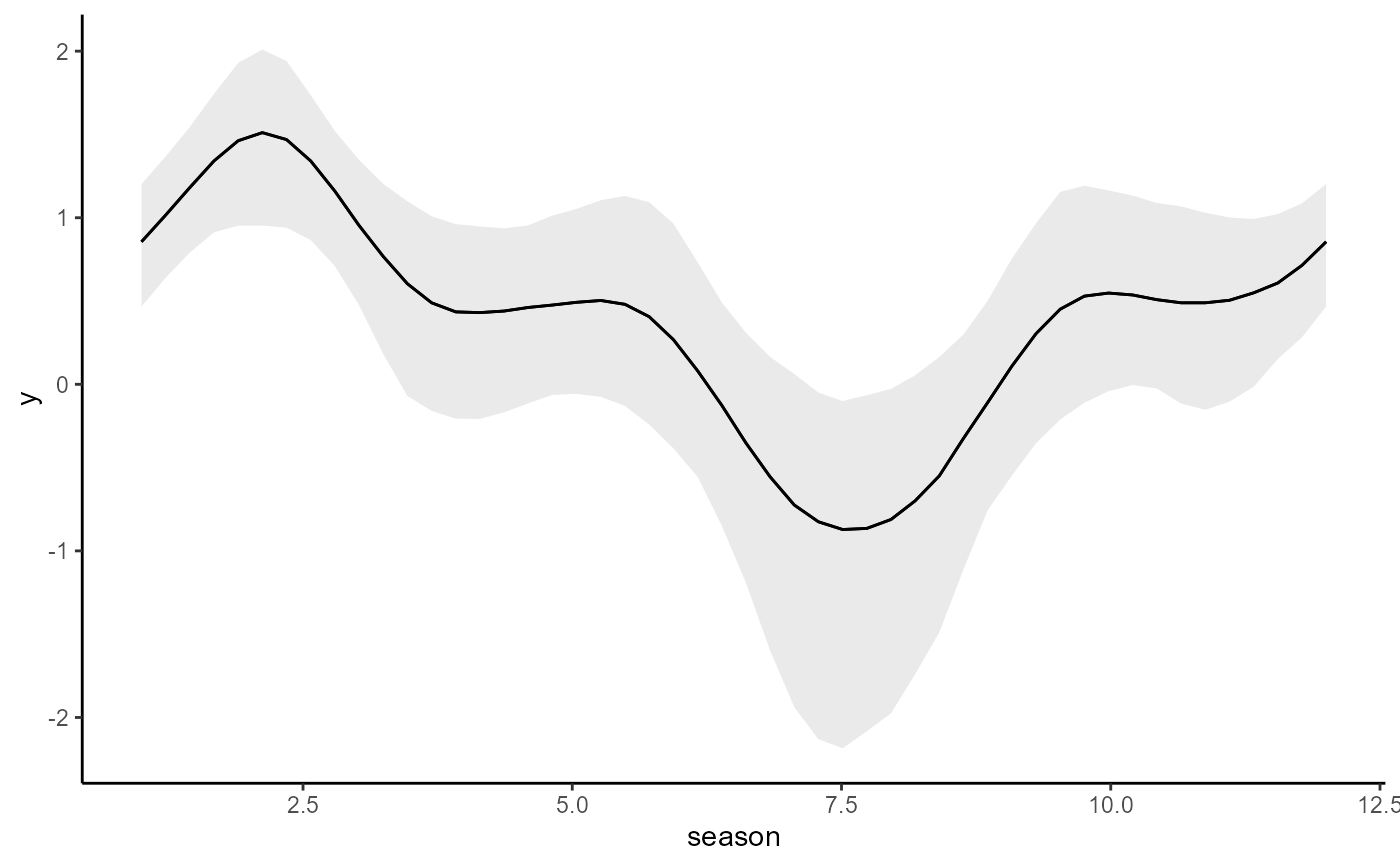# Update to an AR2 model
updated_mod <- update(mod, trend_model = AR(p = 2),
                      noncentred = TRUE)
#> Compiling Stan program using cmdstanr
#> 
#> Start sampling
#> Running MCMC with 2 parallel chains...
#> 
#> Chain 1 Iteration:   1 / 1000 [  0%]  (Warmup) 
#> Chain 1 Iteration: 100 / 1000 [ 10%]  (Warmup) 
#> Chain 2 Iteration:   1 / 1000 [  0%]  (Warmup) 
#> Chain 1 Iteration: 200 / 1000 [ 20%]  (Warmup) 
#> Chain 1 Iteration: 300 / 1000 [ 30%]  (Warmup) 
#> Chain 1 Iteration: 400 / 1000 [ 40%]  (Warmup) 
#> Chain 2 Iteration: 100 / 1000 [ 10%]  (Warmup) 
#> Chain 2 Iteration: 200 / 1000 [ 20%]  (Warmup) 
#> Chain 1 Iteration: 500 / 1000 [ 50%]  (Warmup) 
#> Chain 1 Iteration: 501 / 1000 [ 50%]  (Sampling) 
#> Chain 2 Iteration: 300 / 1000 [ 30%]  (Warmup) 
#> Chain 2 Iteration: 400 / 1000 [ 40%]  (Warmup) 
#> Chain 1 Iteration: 600 / 1000 [ 60%]  (Sampling) 
#> Chain 2 Iteration: 500 / 1000 [ 50%]  (Warmup) 
#> Chain 2 Iteration: 501 / 1000 [ 50%]  (Sampling) 
#> Chain 1 Iteration: 700 / 1000 [ 70%]  (Sampling) 
#> Chain 2 Iteration: 600 / 1000 [ 60%]  (Sampling) 
#> Chain 1 Iteration: 800 / 1000 [ 80%]  (Sampling) 
#> Chain 2 Iteration: 700 / 1000 [ 70%]  (Sampling) 
#> Chain 1 Iteration: 900 / 1000 [ 90%]  (Sampling) 
#> Chain 2 Iteration: 800 / 1000 [ 80%]  (Sampling) 
#> Chain 1 Iteration: 1000 / 1000 [100%]  (Sampling) 
#> Chain 2 Iteration: 900 / 1000 [ 90%]  (Sampling) 
#> Chain 1 finished in 1.0 seconds.
#> Chain 2 Iteration: 1000 / 1000 [100%]  (Sampling) 
#> Chain 2 finished in 1.0 seconds.
#> 
#> Both chains finished successfully.
#> Mean chain execution time: 1.0 seconds.
#> Total execution time: 1.4 seconds.
#> 
summary(updated_mod)
#> GAM formula:
#> y ~ s(season, bs = "cc")
#> <environment: 0x0000024db9be6178>
#> 
#> Family:
#> poisson
#> 
#> Link function:
#> log
#> 
#> Trend model:
#> AR(p = 2)
#> 
#> 
#> N series:
#> 1 
#> 
#> N timepoints:
#> 75 
#> 
#> Status:
#> Fitted using Stan 
#> 2 chains, each with iter = 1000; warmup = 500; thin = 1 
#> Total post-warmup draws = 1000
#> 
#> 
#> GAM coefficient (beta) estimates:
#>              2.5%    50%  97.5% Rhat n_eff
#> (Intercept) -0.76 -0.370 -0.068 1.01   466
#> s(season).1  0.27  0.710  1.300 1.00   681
#> s(season).2 -0.70  0.063  0.590 1.00   744
#> s(season).3 -1.10 -0.340  0.250 1.00   609
#> s(season).4 -0.99 -0.350  0.300 1.00   726
#> s(season).5 -1.00 -0.390  0.340 1.00   859
#> s(season).6 -1.30 -0.690 -0.035 1.00   931
#> s(season).7 -1.40 -0.700 -0.081 1.00   756
#> s(season).8 -1.10 -0.340  0.160 1.00   719
#> 
#> Approximate significance of GAM smooths:
#>            edf Ref.df Chi.sq p-value
#> s(season) 2.73      8   22.1    0.18
#> 
#> Latent trend AR parameter estimates:
#>            2.5%    50% 97.5% Rhat n_eff
#> ar1[1]   -0.950 -0.490  0.55 1.01   318
#> ar2[1]   -0.840  0.099  0.93 1.01   352
#> sigma[1]  0.088  0.490  0.90 1.01   183
#> 
#> Stan MCMC diagnostics:
#> n_eff / iter looks reasonable for all parameters
#> Rhat looks reasonable for all parameters
#> 0 of 1000 iterations ended with a divergence (0%)
#> 0 of 1000 iterations saturated the maximum tree depth of 10 (0%)
#> E-FMI indicated no pathological behavior
#> 
#> Samples were drawn using NUTS(diag_e) at Mon Nov 18 10:37:46 AM 2024.
#> For each parameter, n_eff is a crude measure of effective sample size,
#> and Rhat is the potential scale reduction factor on split MCMC chains
#> (at convergence, Rhat = 1)
conditional_effects(updated_mod, type = 'link')


# Now update to a Binomial AR1 by adding information on trials
# requires that we supply newdata that contains the 'trials' variable
simdat$data_train$trials <- max(simdat$data_train$y) + 15
updated_mod <- update(mod,
                      formula = cbind(y, trials) ~ s(season, bs = 'cc'),
                      noncentred = TRUE,
                      data = simdat$data_train,
                      family = binomial())
#> Compiling Stan program using cmdstanr
#> 
#> Start sampling
#> Running MCMC with 2 parallel chains...
#> 
#> Chain 1 Iteration:   1 / 1000 [  0%]  (Warmup) 
#> Chain 1 Iteration: 100 / 1000 [ 10%]  (Warmup) 
#> Chain 2 Iteration:   1 / 1000 [  0%]  (Warmup) 
#> Chain 1 Iteration: 200 / 1000 [ 20%]  (Warmup) 
#> Chain 1 Iteration: 300 / 1000 [ 30%]  (Warmup) 
#> Chain 1 Iteration: 400 / 1000 [ 40%]  (Warmup) 
#> Chain 2 Iteration: 100 / 1000 [ 10%]  (Warmup) 
#> Chain 2 Iteration: 200 / 1000 [ 20%]  (Warmup) 
#> Chain 1 Iteration: 500 / 1000 [ 50%]  (Warmup) 
#> Chain 1 Iteration: 501 / 1000 [ 50%]  (Sampling) 
#> Chain 1 Iteration: 600 / 1000 [ 60%]  (Sampling) 
#> Chain 2 Iteration: 300 / 1000 [ 30%]  (Warmup) 
#> Chain 2 Iteration: 400 / 1000 [ 40%]  (Warmup) 
#> Chain 1 Iteration: 700 / 1000 [ 70%]  (Sampling) 
#> Chain 2 Iteration: 500 / 1000 [ 50%]  (Warmup) 
#> Chain 2 Iteration: 501 / 1000 [ 50%]  (Sampling) 
#> Chain 1 Iteration: 800 / 1000 [ 80%]  (Sampling) 
#> Chain 2 Iteration: 600 / 1000 [ 60%]  (Sampling) 
#> Chain 2 Iteration: 700 / 1000 [ 70%]  (Sampling) 
#> Chain 1 Iteration: 900 / 1000 [ 90%]  (Sampling) 
#> Chain 1 Iteration: 1000 / 1000 [100%]  (Sampling) 
#> Chain 2 Iteration: 800 / 1000 [ 80%]  (Sampling) 
#> Chain 1 finished in 0.8 seconds.
#> Chain 2 Iteration: 900 / 1000 [ 90%]  (Sampling) 
#> Chain 2 Iteration: 1000 / 1000 [100%]  (Sampling) 
#> Chain 2 finished in 0.8 seconds.
#> 
#> Both chains finished successfully.
#> Mean chain execution time: 0.8 seconds.
#> Total execution time: 1.3 seconds.
#> 
summary(updated_mod)
#> GAM formula:
#> cbind(y, trials) ~ s(season, bs = "cc")
#> <environment: 0x0000024db9be6178>
#> 
#> Family:
#> binomial
#> 
#> Link function:
#> logit
#> 
#> Trend model:
#> AR()
#> 
#> 
#> N series:
#> 1 
#> 
#> N timepoints:
#> 75 
#> 
#> Status:
#> Fitted using Stan 
#> 2 chains, each with iter = 1000; warmup = 500; thin = 1 
#> Total post-warmup draws = 1000
#> 
#> 
#> GAM coefficient (beta) estimates:
#>              2.5%    50%  97.5% Rhat n_eff
#> (Intercept) -3.80 -3.400 -3.100 1.00   645
#> s(season).1  0.22  0.710  1.300 1.00   479
#> s(season).2 -0.58  0.078  0.710 1.00   610
#> s(season).3 -1.10 -0.340  0.320 1.01   509
#> s(season).4 -1.10 -0.370  0.260 1.00   528
#> s(season).5 -1.10 -0.440  0.330 1.01   404
#> s(season).6 -1.50 -0.700 -0.110 1.00   605
#> s(season).7 -1.50 -0.730 -0.048 1.00   510
#> s(season).8 -1.10 -0.340  0.220 1.00   419
#> 
#> Approximate significance of GAM smooths:
#>            edf Ref.df Chi.sq p-value  
#> s(season) 4.25      8   19.6   0.041 *
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Latent trend parameter AR estimates:
#>           2.5%   50% 97.5% Rhat n_eff
#> ar1[1]   -0.97 -0.53  0.31 1.01   351
#> sigma[1]  0.27  0.65  1.10 1.00   320
#> 
#> Stan MCMC diagnostics:
#> n_eff / iter looks reasonable for all parameters
#> Rhat looks reasonable for all parameters
#> 0 of 1000 iterations ended with a divergence (0%)
#> 0 of 1000 iterations saturated the maximum tree depth of 10 (0%)
#> E-FMI indicated no pathological behavior
#> 
#> Samples were drawn using NUTS(diag_e) at Mon Nov 18 10:38:34 AM 2024.
#> For each parameter, n_eff is a crude measure of effective sample size,
#> and Rhat is the potential scale reduction factor on split MCMC chains
#> (at convergence, Rhat = 1)
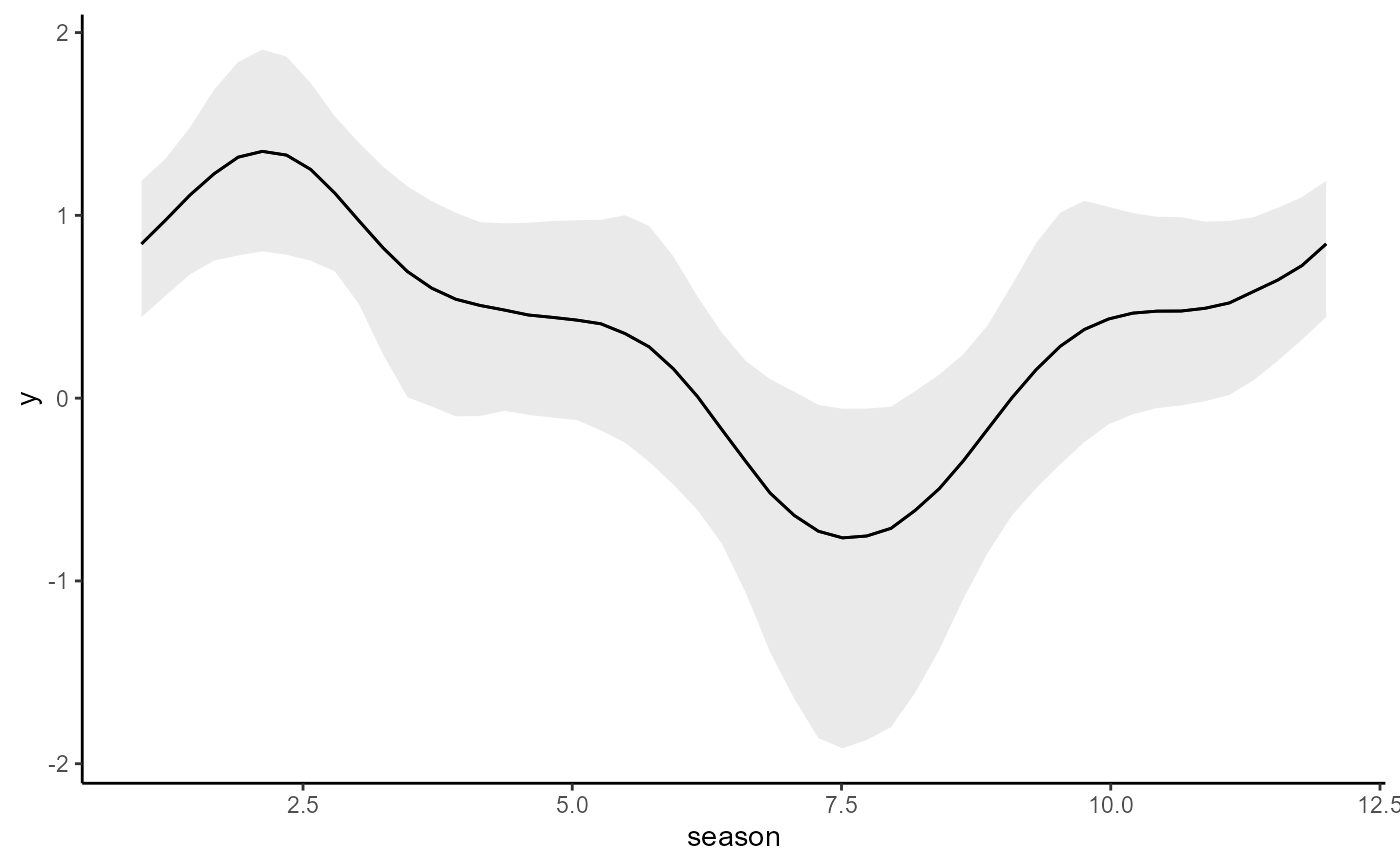
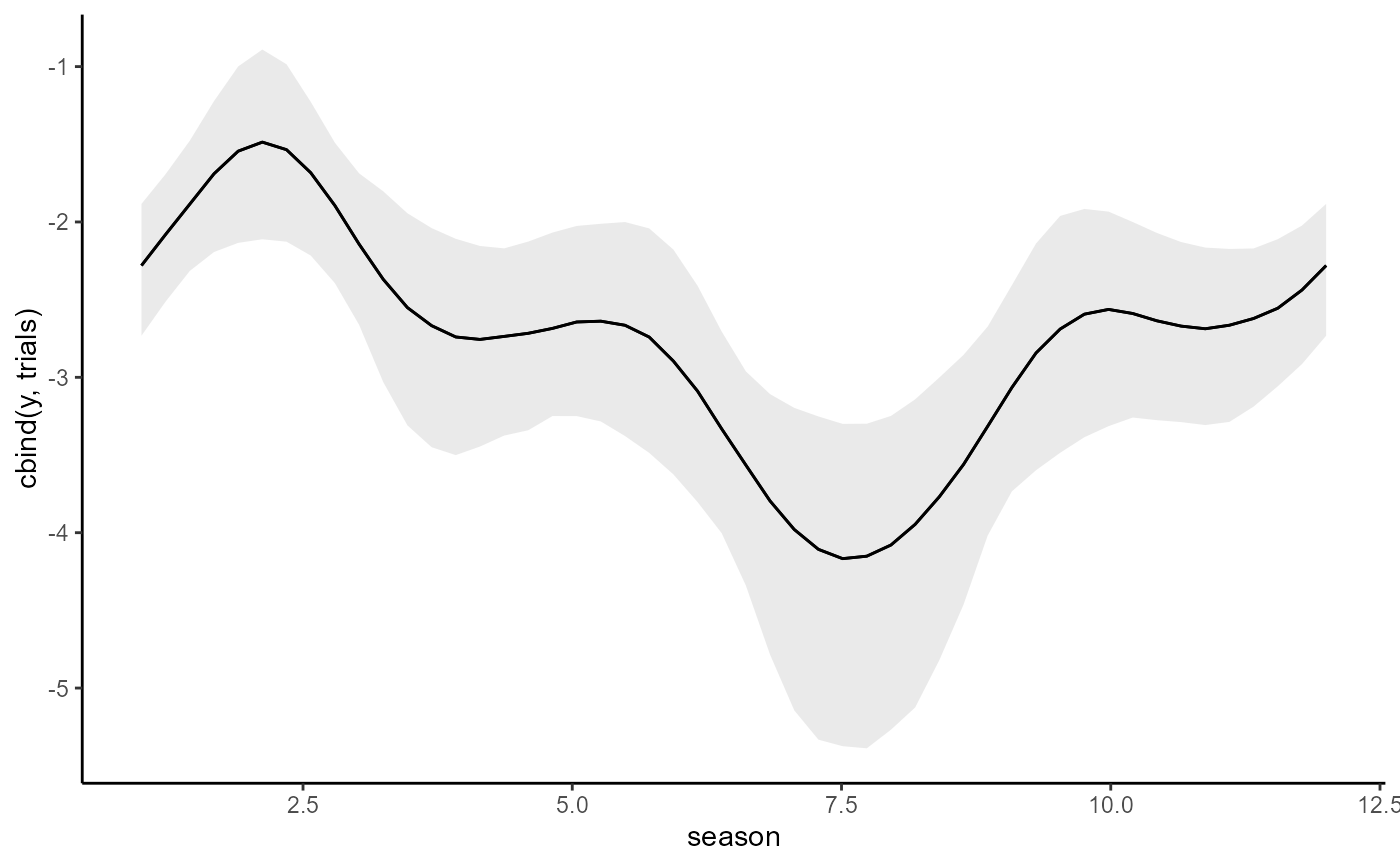
conditional_effects(updated_mod, type = 'link')

# }