Skip to contents

Simulate a set of discrete time series for mvgam modelling

Source: R/sim_mvgam.R
sim_mvgam.Rd

This function simulates discrete time series data for fitting a multivariate GAM that includes shared seasonality and dependence on state-space latent dynamic factors. Random dependencies among series, i.e. correlations in their long-term trends, are included in the form of correlated loadings on the latent dynamic factors

Usage

sim_mvgam(
  T = 100,
  n_series = 3,
  seasonality = "shared",
  use_lv = FALSE,
  n_lv = 1,
  trend_model = "RW",
  drift = FALSE,
  prop_trend = 0.2,
  trend_rel,
  freq = 12,
  family = poisson(),
  phi,
  shape,
  sigma,
  nu,
  mu,
  prop_missing = 0,
  prop_train = 0.85
)

Arguments

T

integer. Number of observations (timepoints)

n_series

integer. Number of discrete time series

seasonality

character. Either shared, meaning that all series share the exact same seasonal pattern, or hierarchical, meaning that there is a global seasonality but each series' pattern can deviate slightly

use_lv

logical. If TRUE, use dynamic factors to estimate series' latent trends in a reduced dimension format. If FALSE, estimate independent latent trends for each series

n_lv

integer. Number of latent dynamic factors for generating the series' trends

trend_model

character specifying the time series dynamics for the latent trend. Options are:

  • None (no latent trend component; i.e. the GAM component is all that contributes to the linear predictor, and the observation process is the only source of error; similarly to what is estimated by gam)

  • RW (random walk with possible drift)

  • AR1 (with possible drift)

  • AR2 (with possible drift)

  • AR3 (with possible drift)

  • VAR1 (contemporaneously uncorrelated VAR1)

  • VAR1cor (contemporaneously correlated VAR1)

  • GP (Gaussian Process with squared exponential kernel)

See mvgam_trends for more details

drift

logical, simulate a drift term for each trend

prop_trend

numeric. Relative importance of the trend for each series. Should be between 0 and 1

trend_rel

Deprecated. Use prop_trend instead

freq

integer. The seasonal frequency of the series

family

family specifying the exponential observation family for the series. Currently supported families are: nb(), poisson(), bernoulli(), tweedie(), gaussian(), betar(), lognormal(), student() and Gamma()

phi

vector of dispersion parameters for the series (i.e. size for nb() or phi for betar()). If length(phi) < n_series, the first element of phi will be replicated n_series times. Defaults to 5 for nb() and tweedie(); 10 for betar()

shape

vector of shape parameters for the series (i.e. shape for gamma()) If length(shape) < n_series, the first element of shape will be replicated n_series times. Defaults to 10

sigma

vector of scale parameters for the series (i.e. sd for gaussian() or student(), log(sd) for lognormal()). If length(sigma) < n_series, the first element of sigma will be replicated n_series times. Defaults to 0.5 for gaussian() and student(); 0.2 for lognormal()

nu

vector of degrees of freedom parameters for the series (i.e. nu for student()) If length(nu) < n_series, the first element of nu will be replicated n_series times. Defaults to 3

mu

vector of location parameters for the series. If length(mu) < n_series, the first element of mu will be replicated n_series times. Defaults to small random values between -0.5 and 0.5 on the link scale

prop_missing

numeric stating proportion of observations that are missing. Should be between 0 and 0.8, inclusive

prop_train

numeric stating the proportion of data to use for training. Should be between 0.2 and 1

Value

A list object containing outputs needed for mvgam, including 'data_train' and 'data_test', as well as some additional information about the simulated seasonality and trend dependencies

Examples

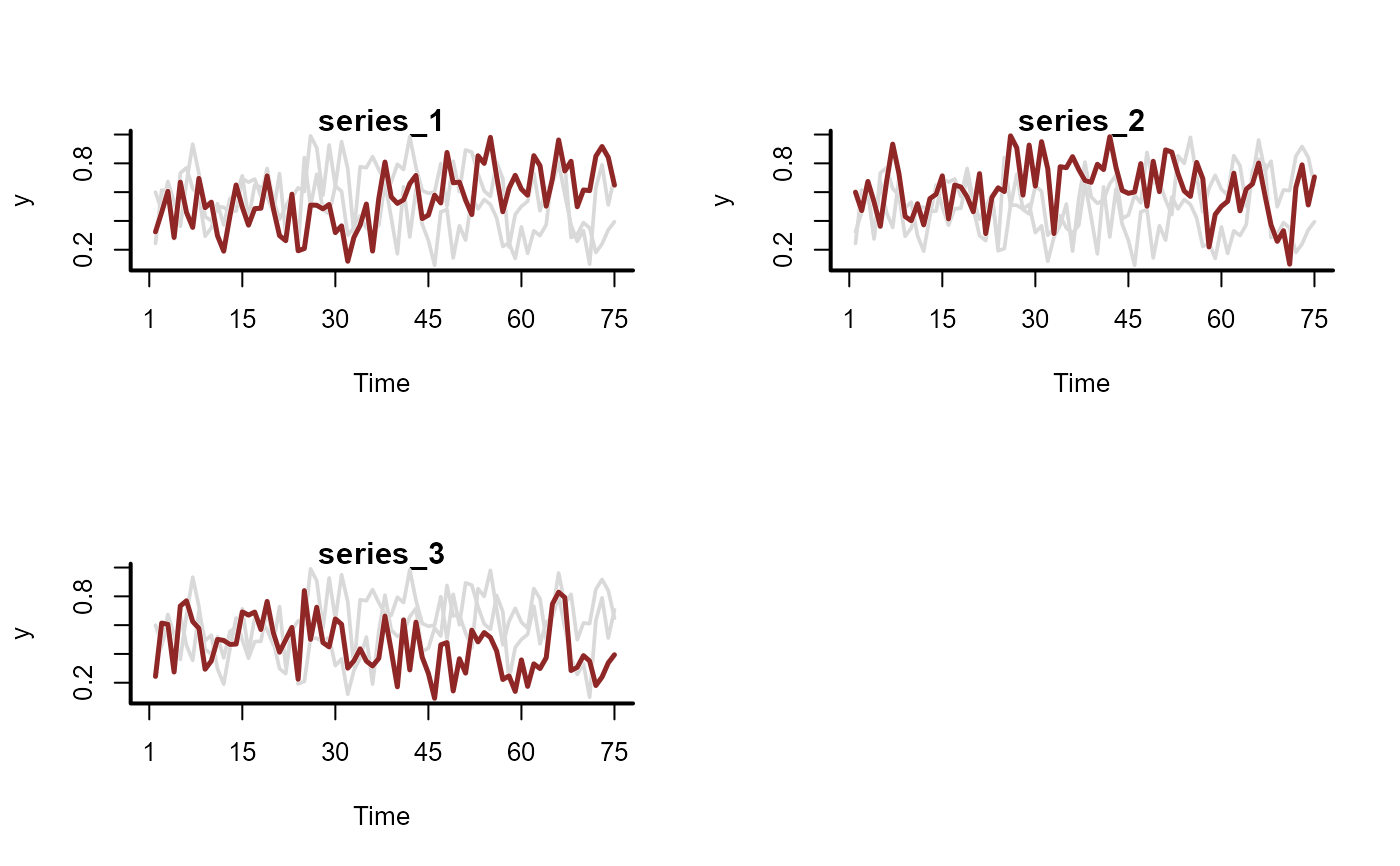
#Simulate series with observations bounded at 0 and 1 (Beta responses)
sim_data <- sim_mvgam(family = betar(), trend_model = 'GP', prop_trend = 0.6)
plot_mvgam_series(data = sim_data$data_train, series = 'all')


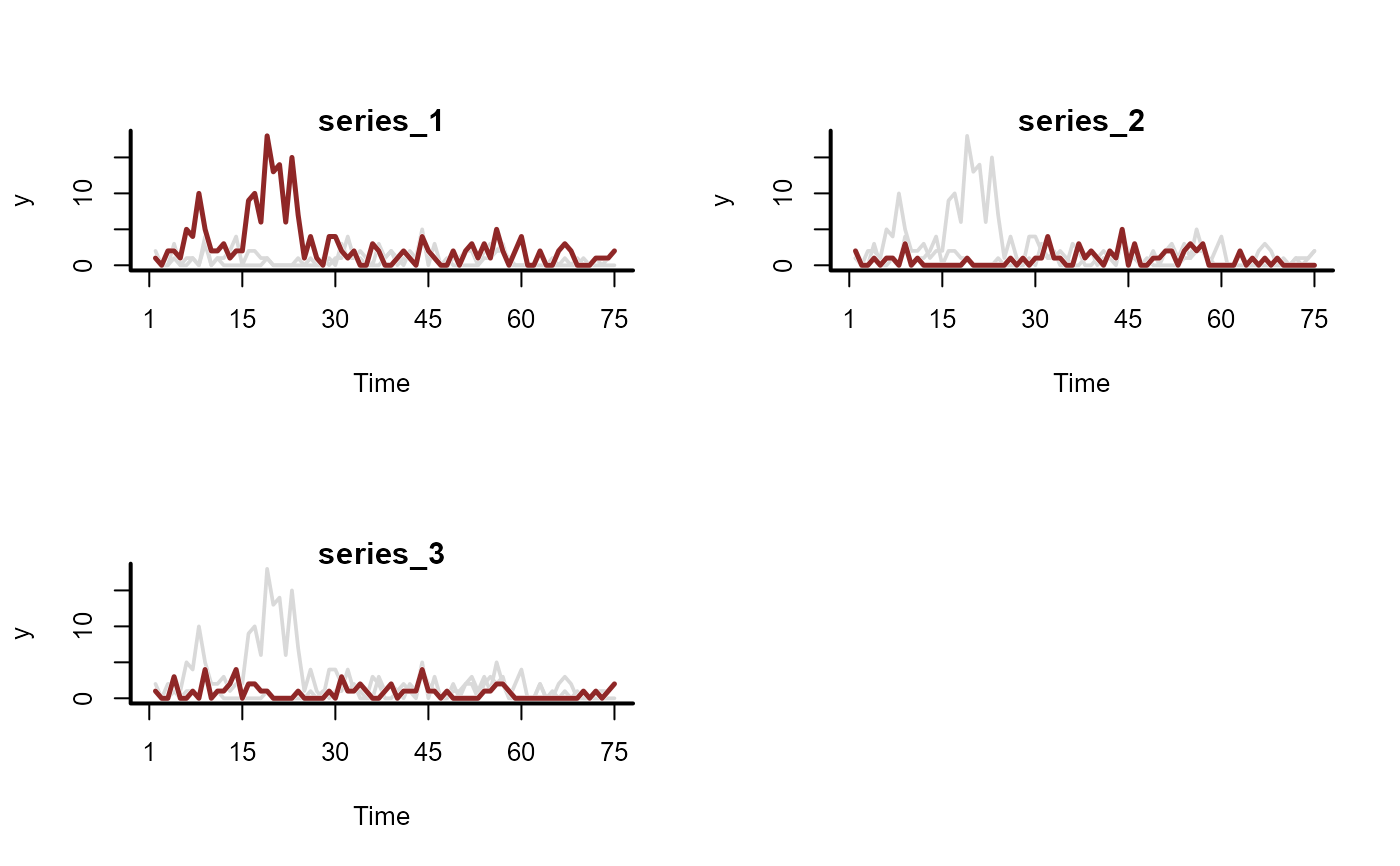
#Now simulate series with overdispersed discrete observations
sim_data <- sim_mvgam(family = nb(), trend_model = 'GP', prop_trend = 0.6, phi = 10)
plot_mvgam_series(data = sim_data$data_train, series = 'all')