Skip to contents

Extract residual correlations based on latent factors

Source: R/residual_cor.R
residual_cor.jsdgam.Rd

Compute residual correlation estimates from Joint Species Distribution (jsdgam) or mvgam models that either used latent factors or included correlated process errors directly

Usage

residual_cor(object, ...)

# S3 method for mvgam
residual_cor(
  object,
  summary = TRUE,
  robust = FALSE,
  probs = c(0.025, 0.975),
  ...
)

# S3 method for jsdgam
residual_cor(
  object,
  summary = TRUE,
  robust = FALSE,
  probs = c(0.025, 0.975),
  ...
)

Arguments

object

list object of class mvgam resulting from a call to jsdgam() or a call to mvgam() in which either use_lv = TRUE or a multivariate process was used with cor = TRUE (see RW() and VAR() for examples)

...

ignored

summary

Should summary statistics be returned instead of the raw values? Default is TRUE..

robust

If FALSE (the default) the mean is used as a measure of central tendency. If TRUE, the median is used instead. Only used if summary is TRUE

probs

The percentiles to be computed by the quantile function. Only used if summary is TRUE.

Value

If summary = TRUE, a list of mvgam_residcor-class with the following components:

cor, cor_lower, cor_upper

A set of \(p \times p\) correlation matrices, containing either the posterior median or mean estimate, plus lower and upper limits of the corresponding credible intervals supplied to probs

sig_cor

A \(p \times p\) correlation matrix containing only correlations whose credible interval does not contain zero. All other correlations are set to zero

prec, prec_lower, prec_upper

A set of \(p \times p\) precision matrices, containing either the posterior median or mean estimate, plus lower and upper limits of the corresponding credible intervals supplied to probs

sig_prec

A \(p \times p\) precision matrix containing only precisions whose credible interval does not contain zero. All other precisions are set to zero

cov

A \(p \times p\) posterior median or mean covariance matrix

trace

The median/mean point estimator of the trace (sum of the diagonal elements) of the residual covariance matrix cov

If summary = FALSE, this function returns a list containing the following components:

all_cormat

A \(n_{draws} \times p \times p\) array of posterior residual correlation matrix draws

all_covmat

A \(n_{draws} \times p \times p\) array of posterior residual covariance matrix draws

all_presmat

A \(n_{draws} \times p \times p\) array of posterior residual precision matrix draws

all_trace

A \(n_{draws}\) vector of posterior covariance trace draws

Details

See mvgam_residcor-class for a description of the quantities that are computed and returned by this function, along with key references.

References

Hui, F. K. C. (2016). boral – Bayesian Ordination and Regression Analysis of Multivariate Abundance Data in r. Methods in Ecology and Evolution, 7(6), 744-750. doi:10.1111/2041-210X.12514

See also

jsdgam(), lv_correlations(), mvgam_residcor-class

Examples

# \donttest{
# Fit a JSDGAM to the portal_data captures
mod <- jsdgam(
  formula = captures ~
    # Fixed effects of NDVI and mintemp, row effect as a GP of time
    ndvi_ma12:series + mintemp:series + gp(time, k = 15),
  factor_formula = ~ -1,
  data = portal_data,
  unit = time,
  species = series,
  family = poisson(),
  n_lv = 2,
  silent = 2,
  chains = 2
)

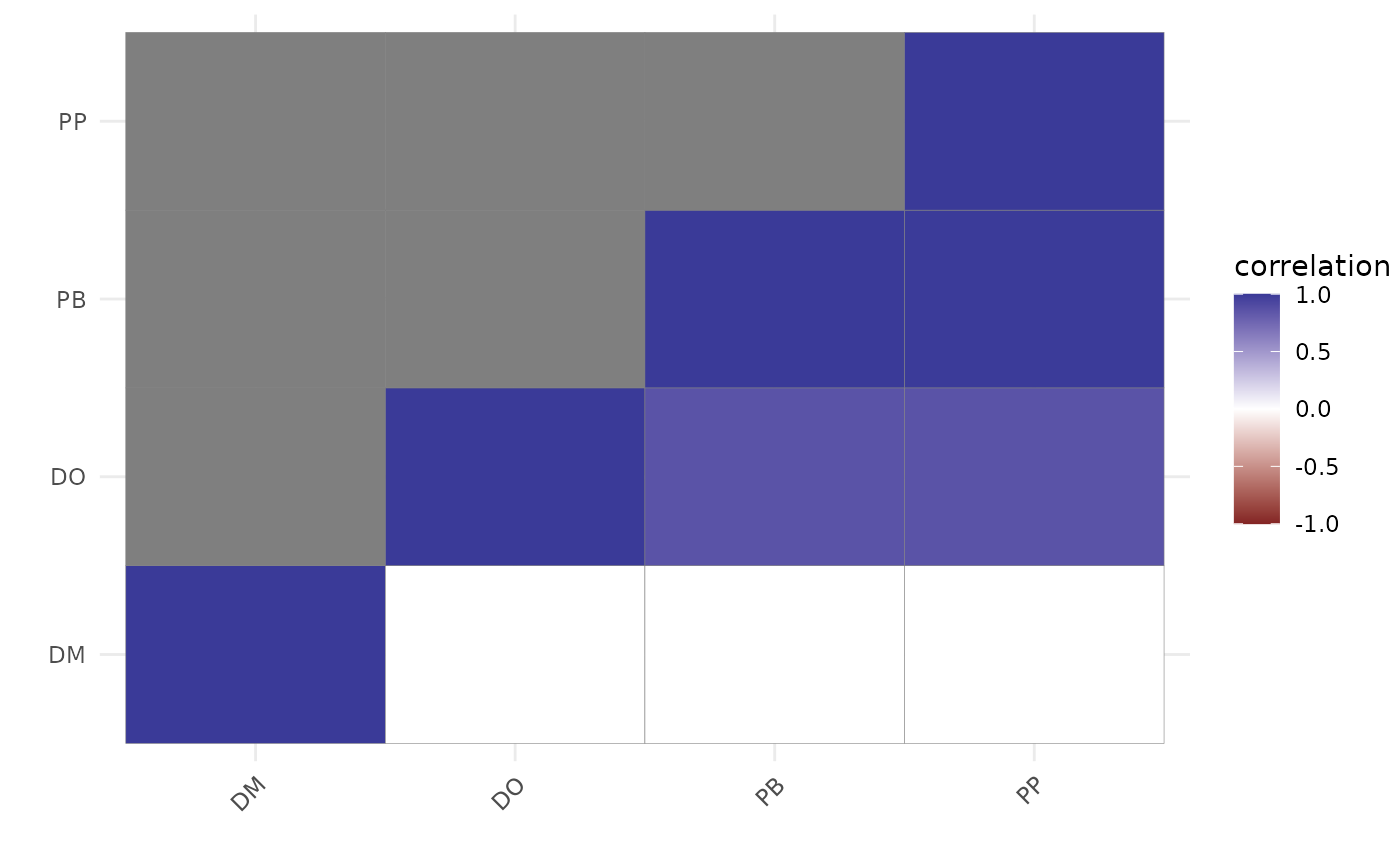
# Plot residual correlations
plot(
  residual_cor(mod)
)


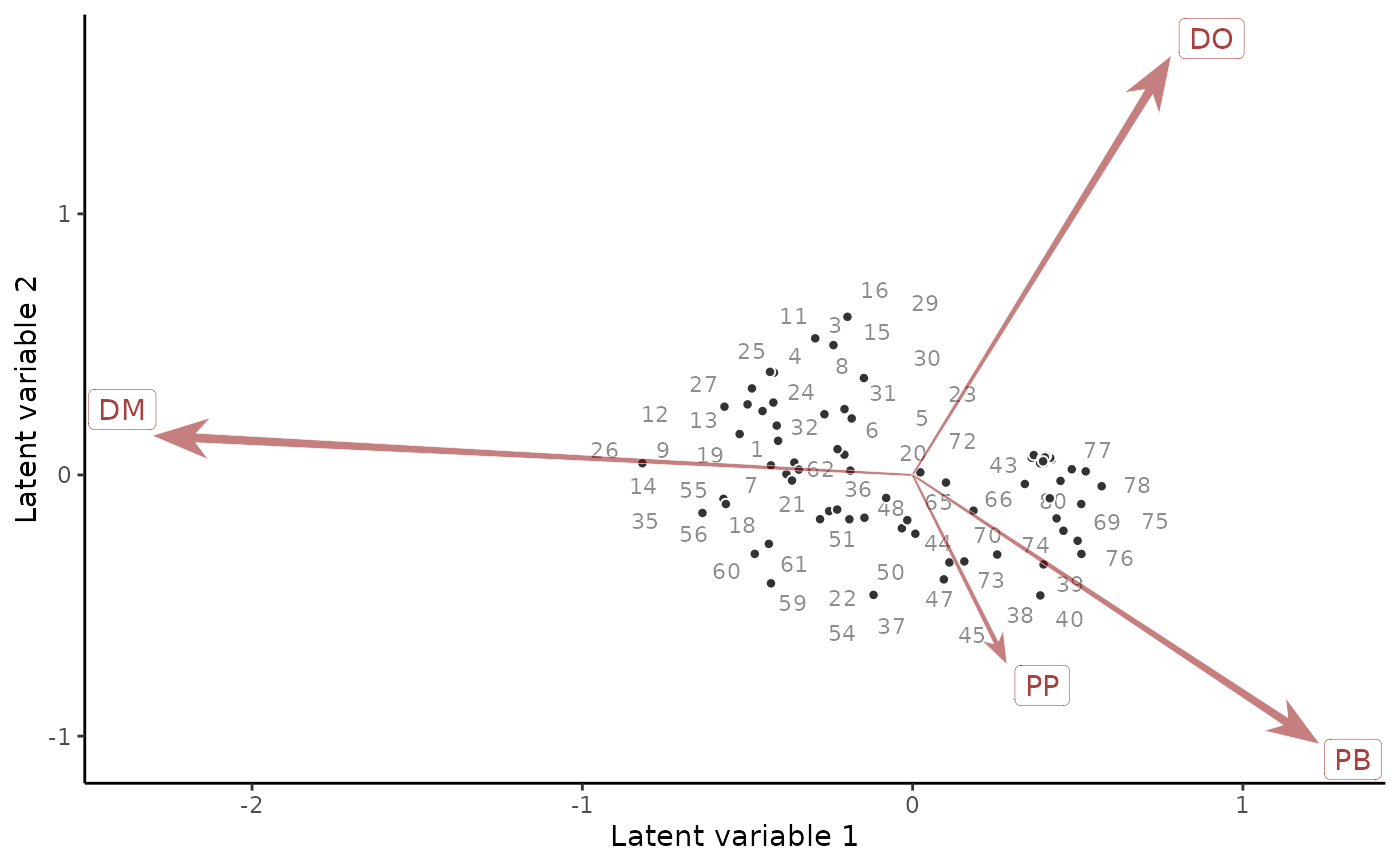
# Compare to a residual ordination biplot
if(requireNamespace('ggrepel', quietly = TRUE)){
  ordinate(mod)
}
#> Warning: ggrepel: 19 unlabeled data points (too many overlaps). Consider increasing max.overlaps

# \dontshow{
# For R CMD check: make sure any open connections are closed afterward
 closeAllConnections()
# }
# }