Calculate latent VAR forecast error variance decompositions

Compute forecast error variance decompositions from mvgam models with Vector Autoregressive dynamics

Usage

fevd(object, ...)

# S3 method for mvgam
fevd(object, h = 10, ...)

Arguments

object

list object of class mvgam resulting from a call to mvgam() that used a Vector Autoregressive latent process model (either as VAR(cor = FALSE) or VAR(cor = TRUE); see VAR() for details)

...

ignored

h

Positive integer specifying the forecast horizon over which to calculate the IRF

Value

See mvgam_fevd-class for a full description of the quantities that are computed and returned by this function, along with key references.

References

Lütkepohl, H. (2007). New Introduction to Multiple Time Series Analysis. 2nd ed. Springer-Verlag Berlin Heidelberg.

See also

VAR(), irf(), stability(), mvgam_fevd-class

Author

Nicholas J Clark

Examples

# \donttest{
# Simulate some time series that follow a latent VAR(1) process
simdat <- sim_mvgam(
  family = gaussian(),
  n_series = 4,
  trend_model = VAR(cor = TRUE),
  prop_trend = 1
)
plot_mvgam_series(data = simdat$data_train, series = "all")


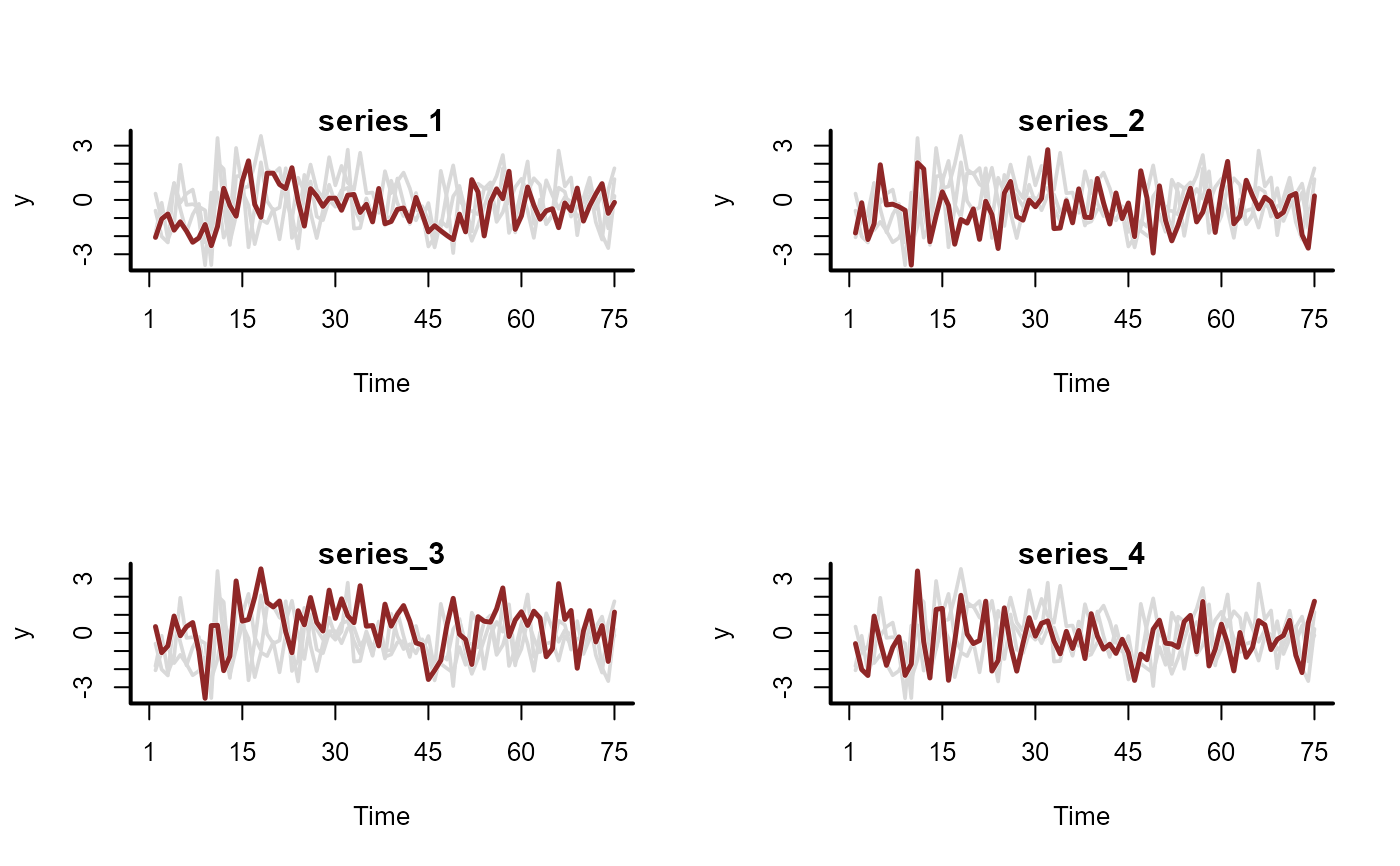# Fit a model that uses a latent VAR(1)
mod <- mvgam(
  formula = y ~ -1,
  trend_formula = ~ 1,
  trend_model = VAR(cor = TRUE),
  family = gaussian(),
  data = simdat$data_train,
  chains = 2,
  silent = 2
)

# Plot the autoregressive coefficient distributions;
# use 'dir = "v"' to arrange the order of facets
# correctly
mcmc_plot(
  mod,
  variable = 'A',
  regex = TRUE,
  type = 'hist',
  facet_args = list(dir = 'v')
)
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.


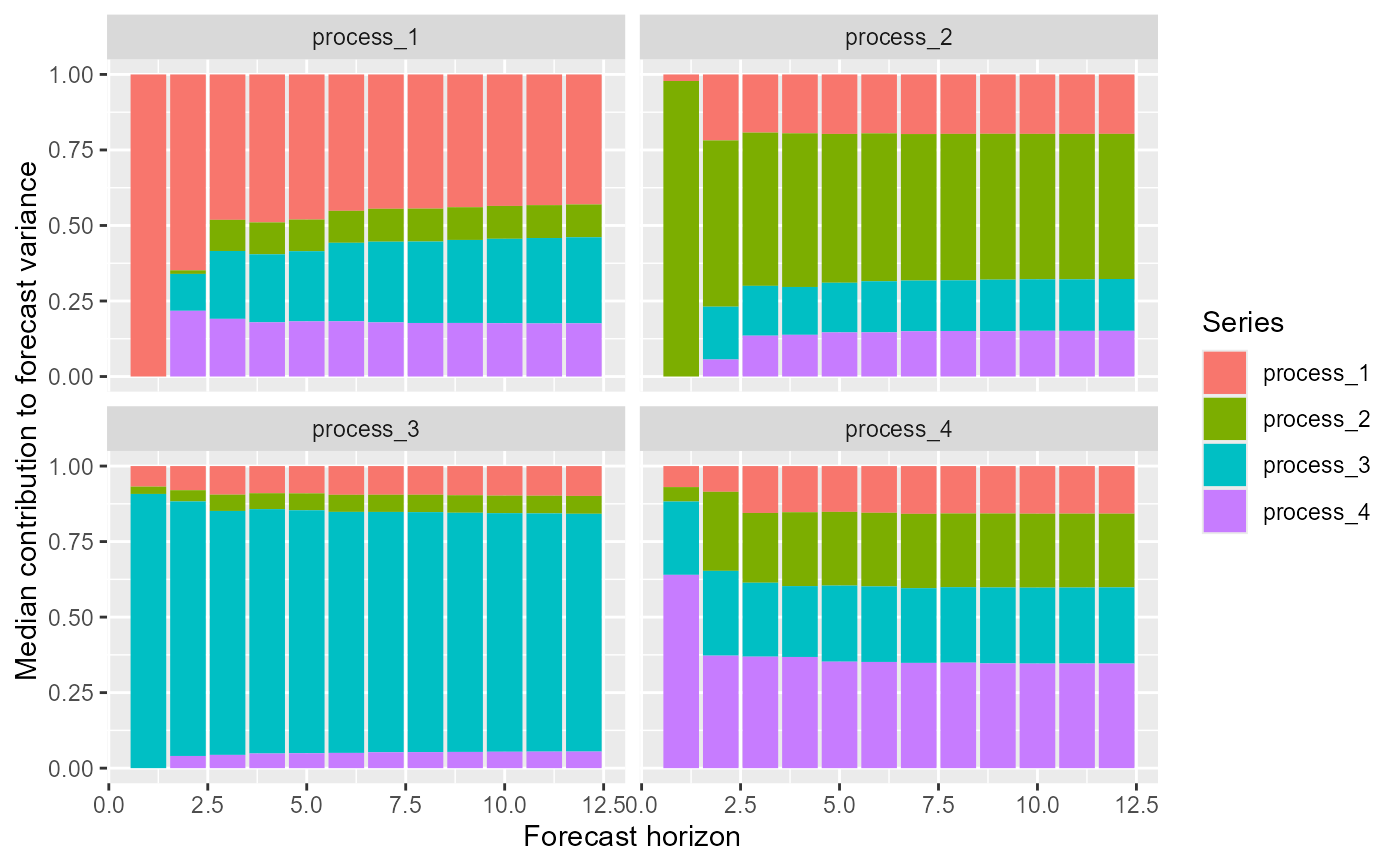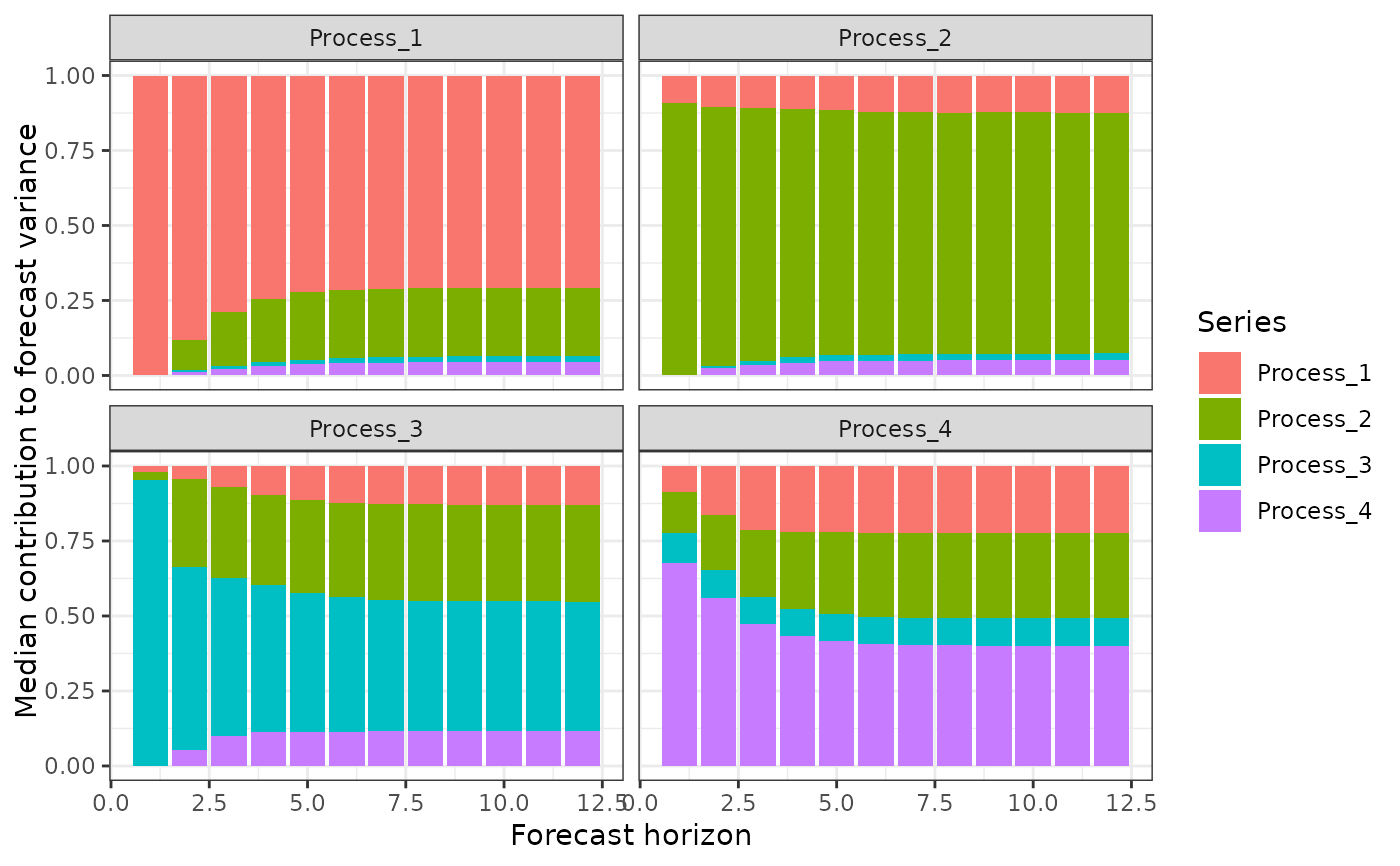
# Calulate forecast error variance decompositions for each series
fevds <- fevd(mod, h = 12)

# Plot median contributions to forecast error variance
plot(fevds)


# View a summary of the error variance decompositions
summary(fevds)
#> # A tibble: 192 × 5
#>    shock                  horizon fevdQ50 fevdQ2.5 fevdQ97.5
#>    <chr>                    <int>   <dbl>    <dbl>     <dbl>
#>  1 Process_1 -> Process_1       1   1        1         1    
#>  2 Process_1 -> Process_1       2   0.936    0.533     0.996
#>  3 Process_1 -> Process_1       3   0.905    0.527     0.992
#>  4 Process_1 -> Process_1       4   0.870    0.488     0.987
#>  5 Process_1 -> Process_1       5   0.841    0.464     0.984
#>  6 Process_1 -> Process_1       6   0.815    0.436     0.979
#>  7 Process_1 -> Process_1       7   0.797    0.419     0.978
#>  8 Process_1 -> Process_1       8   0.780    0.403     0.974
#>  9 Process_1 -> Process_1       9   0.766    0.382     0.973
#> 10 Process_1 -> Process_1      10   0.757    0.375     0.972
#> # ℹ 182 more rows
# }