Evaluate forecasts from fitted mvgam objects
Usage
eval_mvgam(
object,
n_samples = 5000,
eval_timepoint = 3,
fc_horizon = 3,
n_cores = 1,
score = "drps",
log = FALSE,
weights
)
roll_eval_mvgam(
object,
n_evaluations = 5,
evaluation_seq,
n_samples = 5000,
fc_horizon = 3,
n_cores = 1,
score = "drps",
log = FALSE,
weights
)
compare_mvgams(
model1,
model2,
n_samples = 1000,
fc_horizon = 3,
n_evaluations = 10,
n_cores = 1,
score = "drps",
log = FALSE,
weights
)Arguments
- object
listobject returned frommvgam- n_samples
integerspecifying the number of samples to generate from the model's posterior distribution- eval_timepoint
integerindexing the timepoint that represents our last 'observed' set of outcome data- fc_horizon
integerspecifying the length of the forecast horizon for evaluating forecasts- n_cores
Deprecated. Parallel processing is no longer supported
- score
characterspecifying the type of ranked probability score to use for evaluation. Options are:variogram,drpsorcrps- log
logical. Should the forecasts and truths be logged prior to scoring? This is often appropriate for comparing performance of models when series vary in their observation ranges- weights
optional
vectorof weights (wherelength(weights) == n_series) for weighting pairwise correlations when evaluating the variogram score for multivariate forecasts. Useful for down-weighting series that have larger magnitude observations or that are of less interest when forecasting. Ignored ifscore != 'variogram'- n_evaluations
integerspecifying the total number of evaluations to perform- evaluation_seq
Optional
integer sequencespecifying the exact set of timepoints for evaluating the model's forecasts. This sequence cannot have values<3or> max(training timepoints) - fc_horizon- model1
listobject returned frommvgamrepresenting the first model to be evaluated- model2
listobject returned frommvgamrepresenting the second model to be evaluated
Value
For eval_mvgam, a list object containing information on
specific evaluations for each series (if using drps or crps as the score)
or a vector of scores when using variogram.
For roll_eval_mvgam, a list object containing information on specific
evaluations for each series as well as a total evaluation summary (taken by
summing the forecast score for each series at each evaluation and averaging
the coverages at each evaluation)
For compare_mvgams, a series of plots comparing forecast Rank Probability
Scores for each competing model. A lower score is preferred. Note however
that it is possible to select a model that ultimately would perform poorly
in true out-of-sample forecasting. For example if a wiggly smooth function
of 'year' is included in the model then this function will be learned prior
to evaluating rolling window forecasts, and the model could generate very
tight predictions as a result. But when forecasting ahead to timepoints that
the model has not seen (i.e. next year), the smooth function will end up
extrapolating, sometimes in very strange and unexpected ways. It is therefore
recommended to only use smooth functions for covariates that are adequately
measured in the data (i.e. 'seasonality', for example) to reduce possible
extrapolation of smooths and let the latent trends in the mvgam model
capture any temporal dependencies in the data. These trends are time series
models and so will provide much more stable forecasts
Details
eval_mvgam may be useful when both repeated fitting of a model
using update.mvgam for exact leave-future-out cross-validation
and approximate leave-future-out cross-validation using lfo_cv
are impractical. The function generates a set of samples representing fixed
parameters estimated from the full mvgam model and latent trend states
at a given point in time. The trends are rolled forward a total of
fc_horizon timesteps according to their estimated state space dynamics
to generate an 'out-of-sample' forecast that is evaluated against the true
observations in the horizon window. This function therefore simulates a
situation where the model's parameters had already been estimated but we have
only observed data up to the evaluation timepoint and would like to generate
forecasts from the latent trends that have been observed up to that timepoint.
Evaluation involves calculating an appropriate Rank Probability Score and a
binary indicator for whether or not the true value lies within the forecast's
90% prediction interval
roll_eval_mvgam sets up a sequence of evaluation timepoints along a rolling
window and iteratively calls eval_mvgam to evaluate 'out-of-sample'
forecasts. Evaluation involves calculating the Rank Probability Scores and a
binary indicator for whether or not the true value lies within the forecast's
90% prediction interval
compare_mvgams automates the evaluation to compare two fitted models using
rolling window forecast evaluation and provides a series of summary plots to
facilitate model selection. It is essentially a wrapper for
roll_eval_mvgam
Examples
# \donttest{
# Simulate from a Poisson-AR2 model with a seasonal smooth
set.seed(1)
dat <- sim_mvgam(
T = 75,
n_series = 1,
prop_trend = 0.75,
trend_model = AR(p = 2),
family = poisson()
)
# Fit an appropriate model
mod_ar2 <- mvgam(
formula = y ~ s(season, bs = 'cc'),
trend_model = AR(p = 2),
family = poisson(),
data = dat$data_train,
newdata = dat$data_test,
chains = 2,
silent = 2
)
# Fit a less appropriate model
mod_rw <- mvgam(
formula = y ~ 1,
trend_model = RW(),
family = poisson(),
data = dat$data_train,
newdata = dat$data_test,
chains = 2,
silent = 2
)
# Compare Discrete Ranked Probability Scores for the testing period
fc_ar2 <- forecast(mod_ar2)
fc_rw <- forecast(mod_rw)
score_ar2 <- score(
object = fc_ar2,
score = 'drps'
)
score_rw <- score(
object = fc_rw,
score = 'drps'
)
sum(score_ar2$series_1$score)
#> [1] 25.28242
sum(score_rw$series_1$score)
#> [1] 39.65344
# Use rolling evaluation for approximate comparisons of 3-step ahead
# forecasts across the training period
compare_mvgams(
model1 = mod_ar2,
model2 = mod_rw,
fc_horizon = 3,
n_samples = 1000,
n_evaluations = 5
)
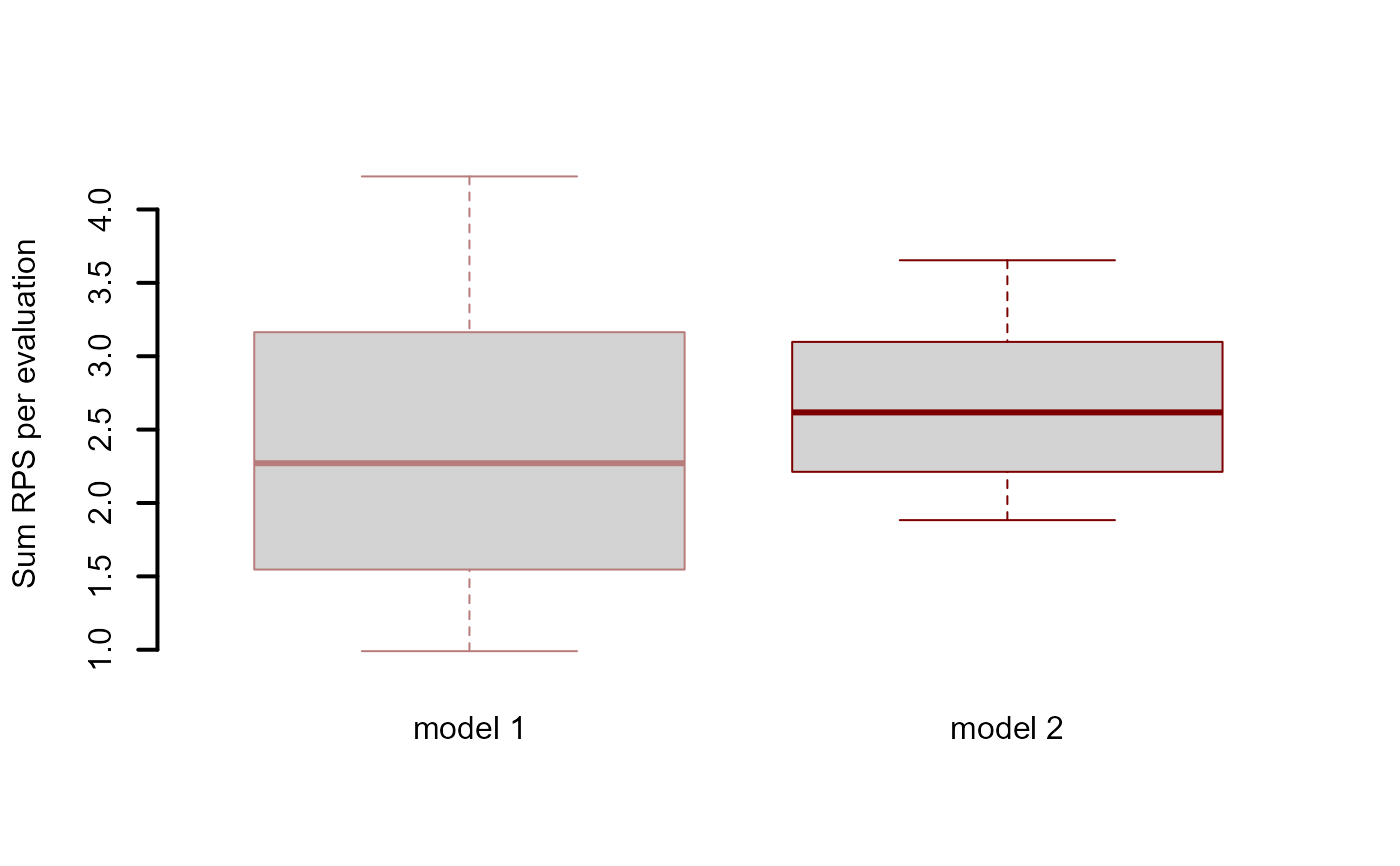
#> RPS summaries per model (lower is better)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> Model 1 0.895669 1.444535 1.993402 2.389999 3.137164 4.280926
#> Model 2 1.840698 2.166373 2.492047 2.534437 2.881306 3.270565
#>
#> 90% interval coverages per model (closer to 0.9 is better)
#> Model 1 0.9333333
#> Model 2 1

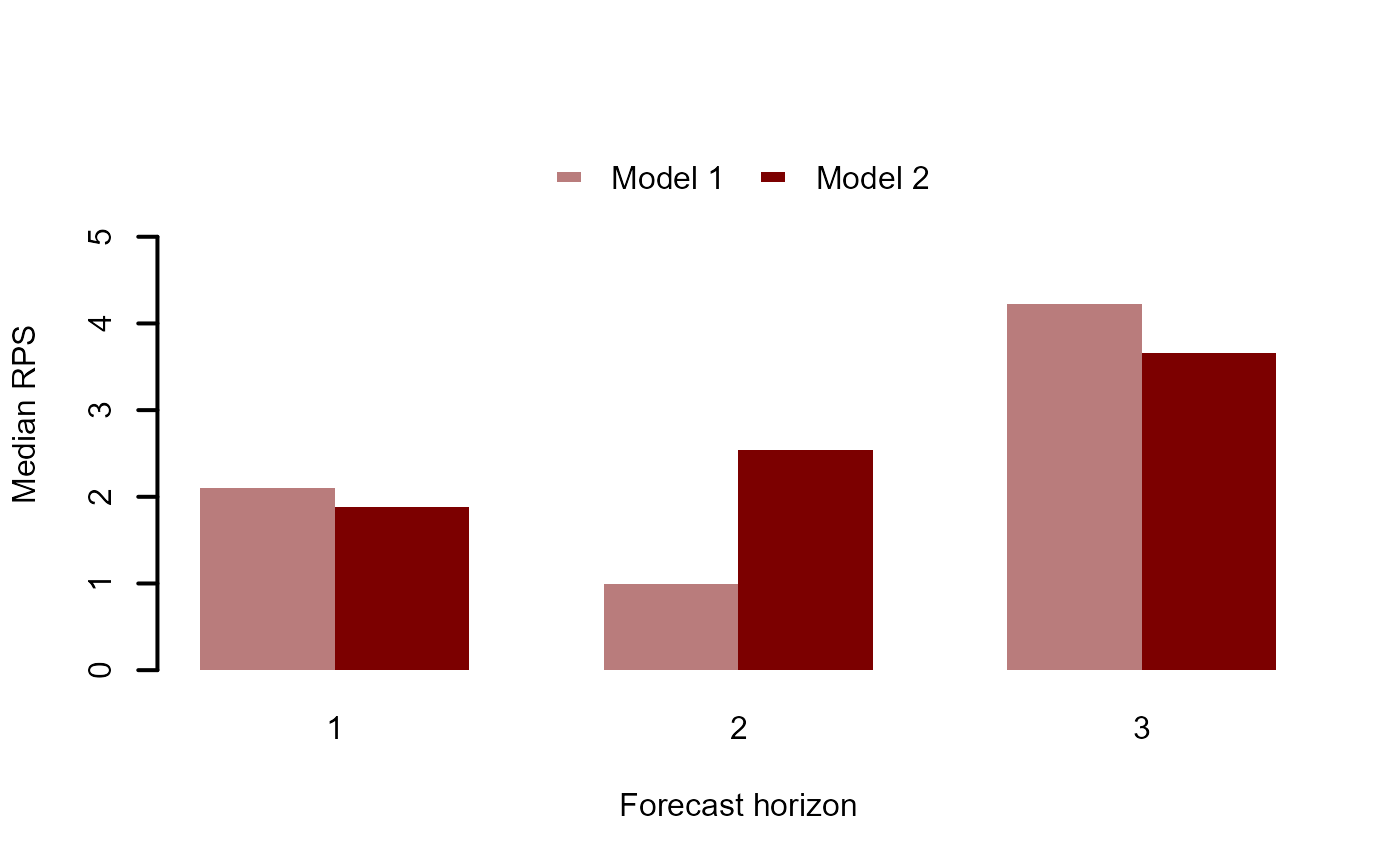 # Now use approximate leave-future-out CV to compare
# rolling forecasts; start at time point 40 to reduce
# computational time and to ensure enough data is available
# for estimating model parameters
lfo_ar2 <- lfo_cv(
object = mod_ar2,
min_t = 40,
fc_horizon = 3,
silent = 2
)
lfo_rw <- lfo_cv(
object = mod_rw,
min_t = 40,
fc_horizon = 3,
silent = 2
)
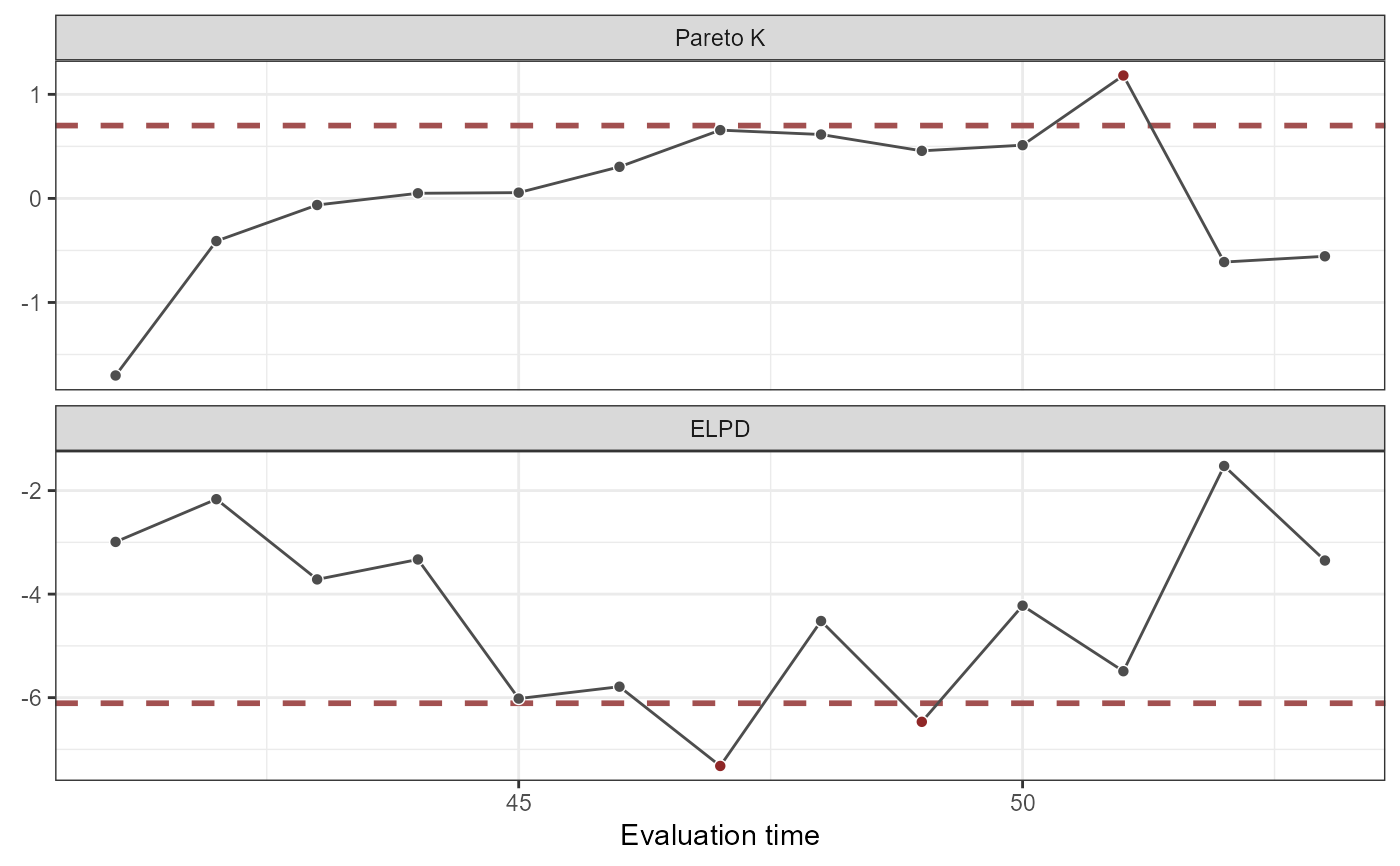
# Plot Pareto-K values and ELPD estimates
plot(lfo_ar2)
# Now use approximate leave-future-out CV to compare
# rolling forecasts; start at time point 40 to reduce
# computational time and to ensure enough data is available
# for estimating model parameters
lfo_ar2 <- lfo_cv(
object = mod_ar2,
min_t = 40,
fc_horizon = 3,
silent = 2
)
lfo_rw <- lfo_cv(
object = mod_rw,
min_t = 40,
fc_horizon = 3,
silent = 2
)
# Plot Pareto-K values and ELPD estimates
plot(lfo_ar2)
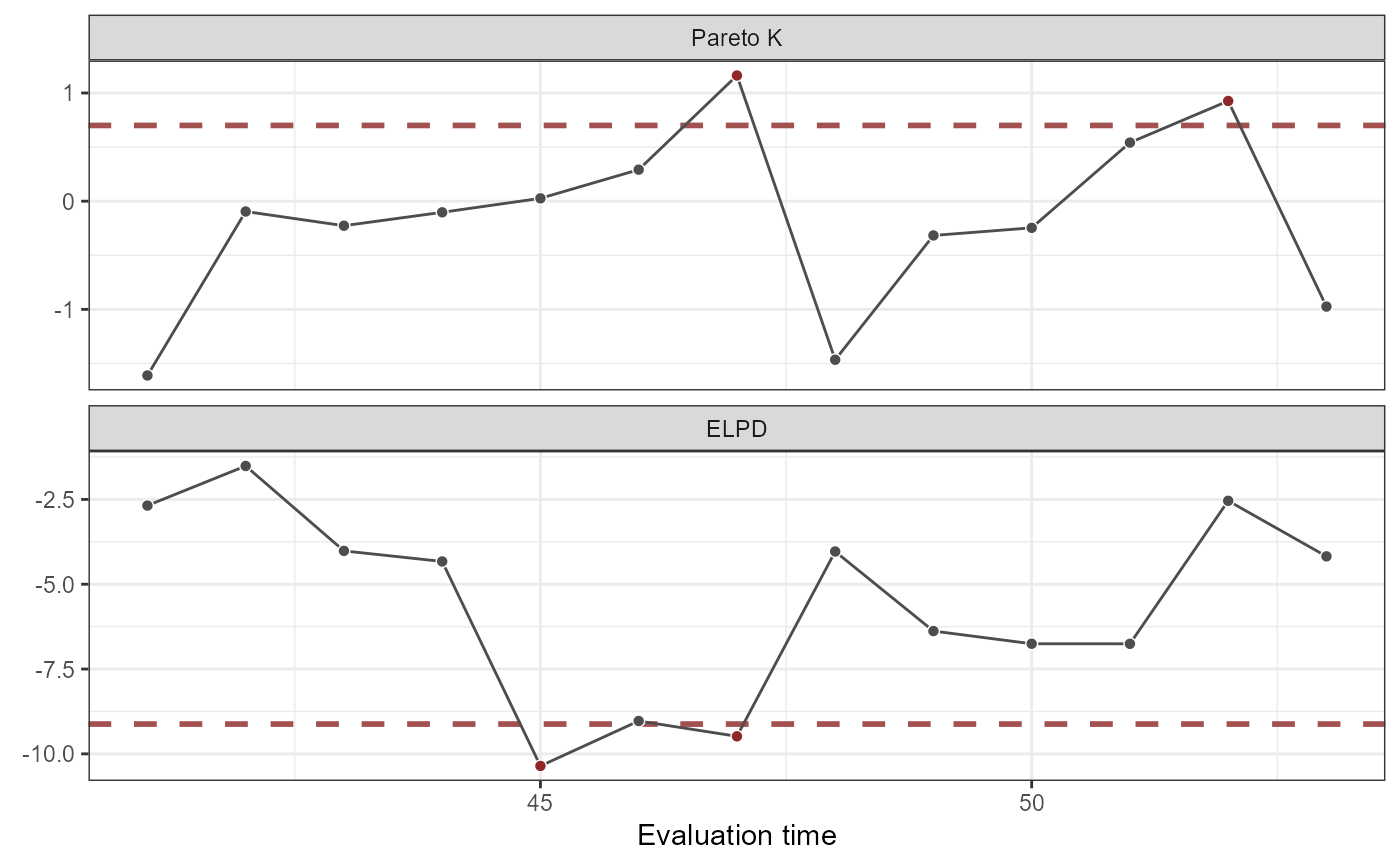
 plot(lfo_rw)
plot(lfo_rw)
 # Proportion of timepoints in which AR2 model gives
# better forecasts
length(which((lfo_ar2$elpds - lfo_rw$elpds) > 0)) /
length(lfo_ar2$elpds)
#> [1] 0.7692308
# A higher total ELPD is preferred
lfo_ar2$sum_ELPD
#> [1] -58.7342
lfo_rw$sum_ELPD
#> [1] -76.57276
# }
# Proportion of timepoints in which AR2 model gives
# better forecasts
length(which((lfo_ar2$elpds - lfo_rw$elpds) > 0)) /
length(lfo_ar2$elpds)
#> [1] 0.7692308
# A higher total ELPD is preferred
lfo_ar2$sum_ELPD
#> [1] -58.7342
lfo_rw$sum_ELPD
#> [1] -76.57276
# }
