Combine forecasts from mvgam models into evenly weighted ensembles
Source:R/ensemble.R
ensemble.mvgam_forecast.RdGenerate evenly weighted ensemble forecast distributions from
mvgam_forecast objects.
Arguments
- object
listobject of classmvgam_forecast. Seeforecast.mvgam()- ...
More
mvgam_forecastobjects.- ndraws
Positive integer specifying the number of draws to use from each forecast distribution for creating the ensemble. If some of the ensemble members have fewer draws than
ndraws, their forecast distributions will be resampled with replacement to achieve the correct number of draws
Value
An object of class mvgam_forecast containing the ensemble
predictions. This object can be readily used with the supplied S3
functions plot and score.
Details
It is widely recognised in the forecasting literature that
combining forecasts from different models often results in improved
forecast accuracy. The simplest way to create an ensemble is to use
evenly weighted combinations of forecasts from the different models.
This is straightforward to do in a Bayesian setting with mvgam as
the posterior MCMC draws contained in each mvgam_forecast object
will already implicitly capture correlations among the temporal posterior
predictions.
Examples
# \dontrun{
# Simulate some series and fit a few competing dynamic models
set.seed(1)
simdat <- sim_mvgam(
n_series = 1,
prop_trend = 0.6,
mu = 1
)
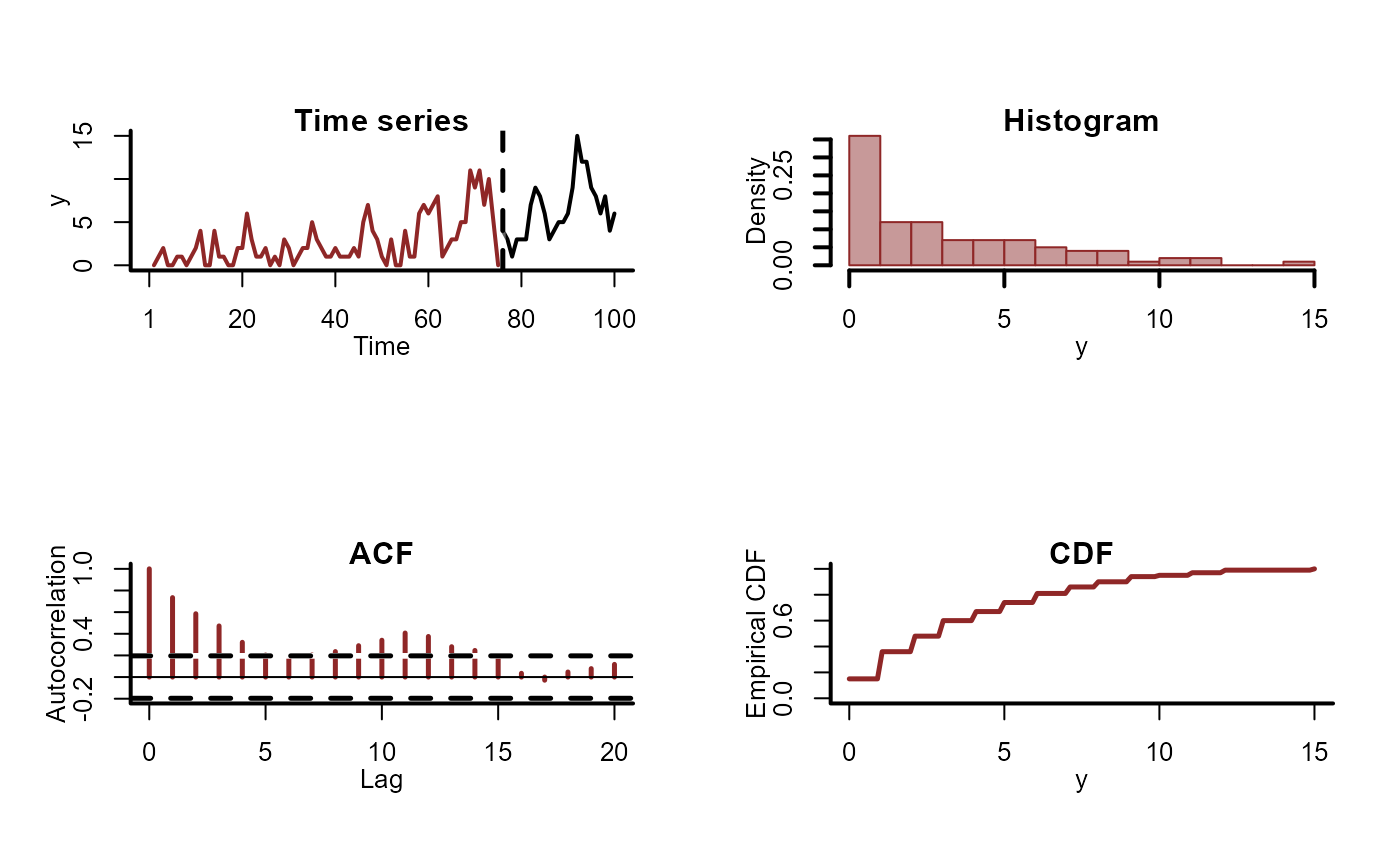
plot_mvgam_series(
data = simdat$data_train,
newdata = simdat$data_test
)
m1 <- mvgam(
y ~ 1,
trend_formula = ~ time +
s(season, bs = 'cc', k = 9),
trend_model = AR(p = 1),
noncentred = TRUE,
data = simdat$data_train,
newdata = simdat$data_test,
chains = 2,
silent = 2
)
m2 <- mvgam(
y ~ time,
trend_model = RW(),
noncentred = TRUE,
data = simdat$data_train,
newdata = simdat$data_test,
chains = 2,
silent = 2
)
# Calculate forecast distributions for each model
fc1 <- forecast(m1)
fc2 <- forecast(m2)
# Generate the ensemble forecast
ensemble_fc <- ensemble(fc1, fc2)
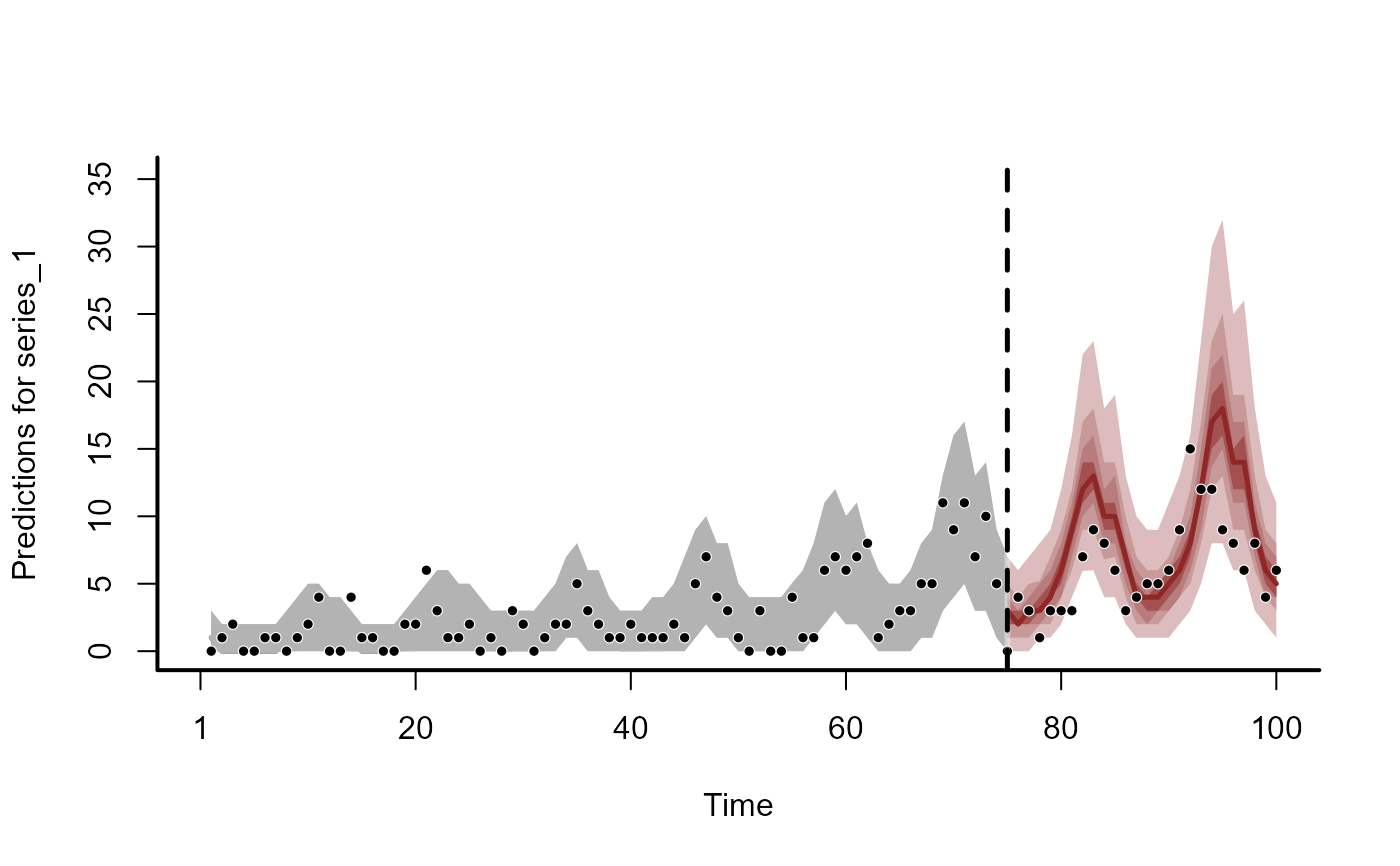
# Plot forecasts
plot(fc1)
#> Out of sample DRPS:
#> 42.972195
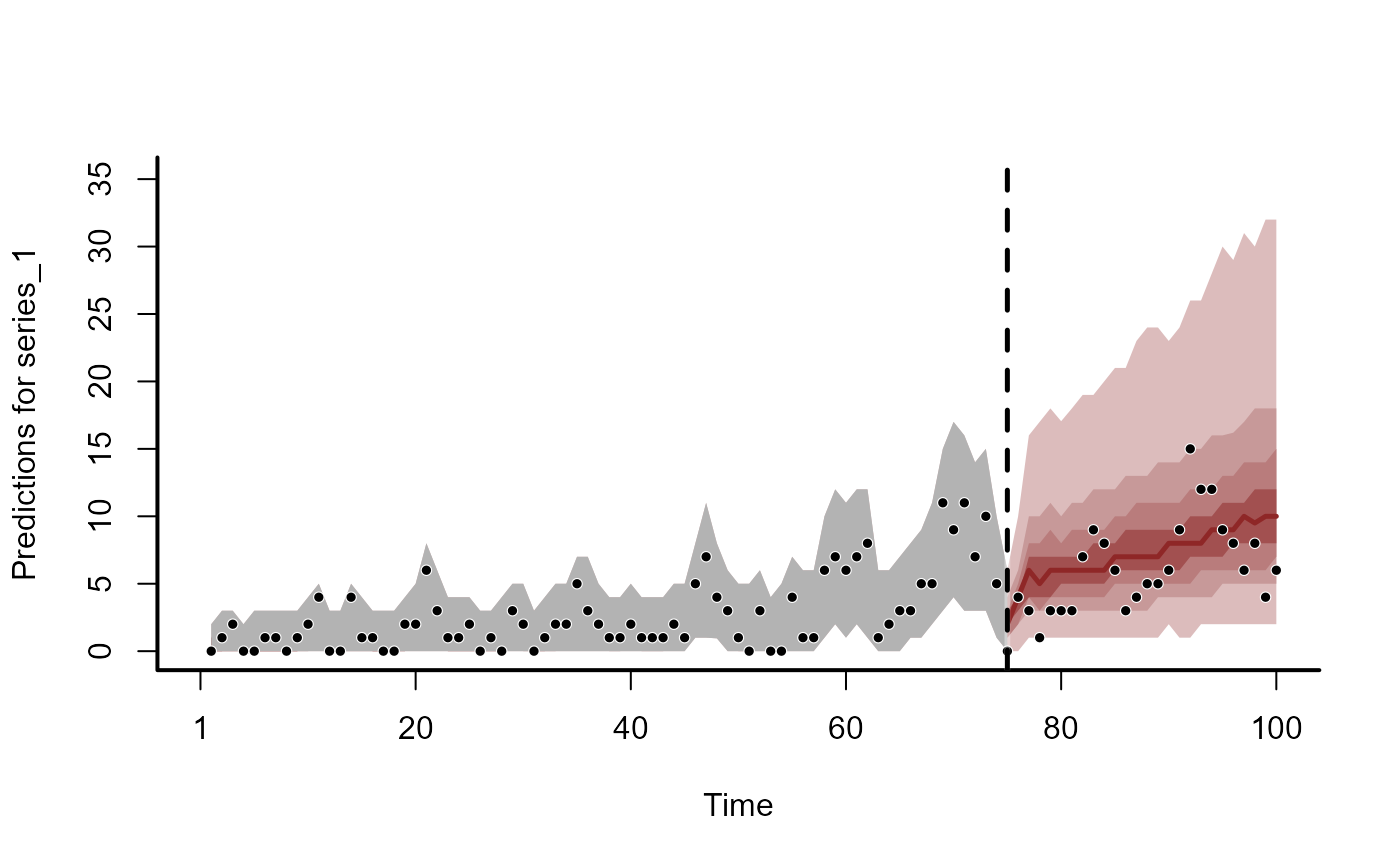
plot(fc2)
#> Out of sample DRPS:
#> 47.85449
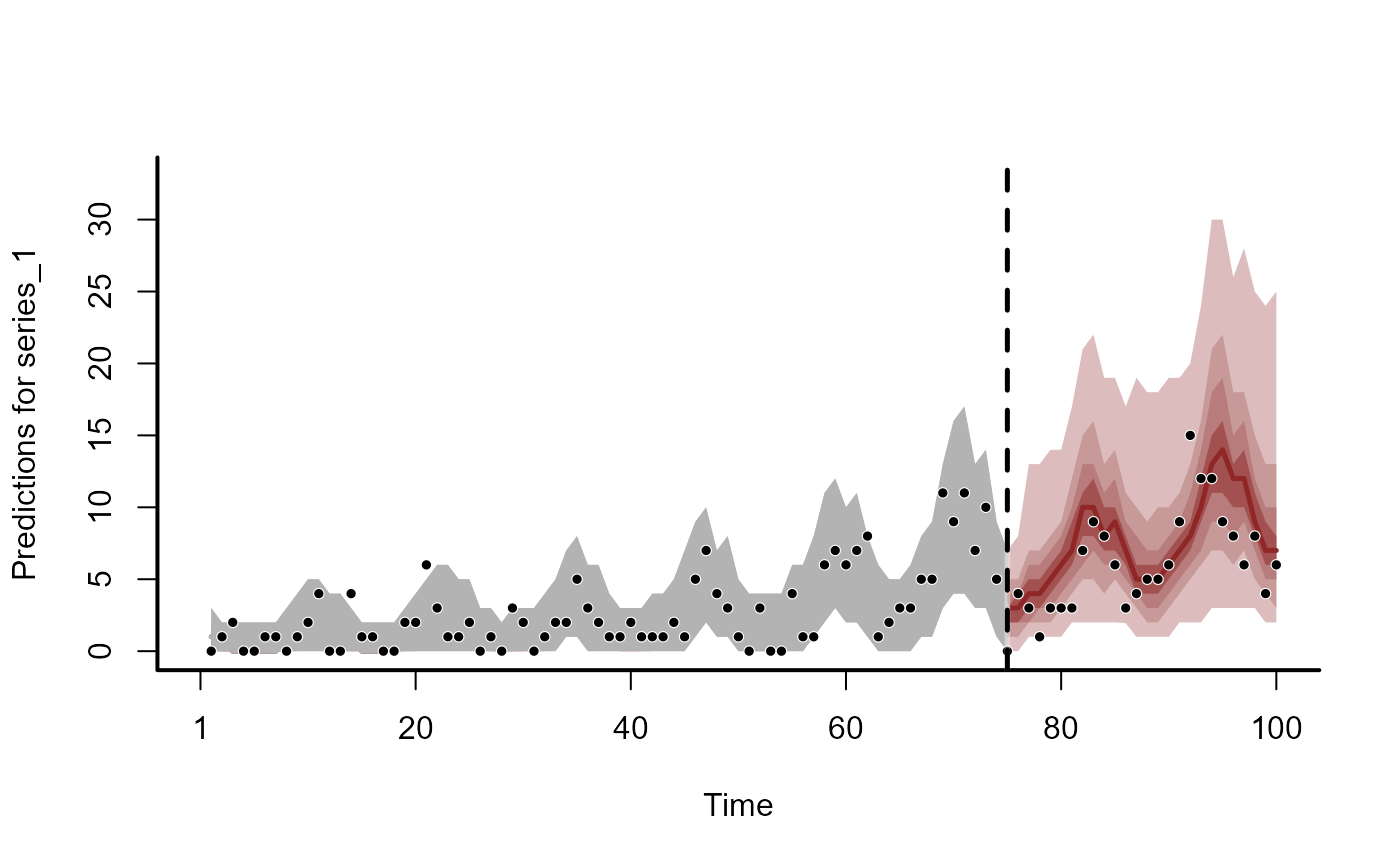
plot(ensemble_fc)
#> Out of sample DRPS:
#> 44.0136756
# Score forecasts
score(fc1)
#> $series_1
#> score in_interval interval_width eval_horizon score_type
#> 1 3.752994 1 0.9 1 crps
#> 2 0.965486 1 0.9 2 crps
#> 3 2.011183 1 0.9 3 crps
#> 4 1.488581 1 0.9 4 crps
#> 5 0.915023 1 0.9 5 crps
#> 6 1.382627 1 0.9 6 crps
#> 7 1.966603 1 0.9 7 crps
#> 8 1.628268 1 0.9 8 crps
#> 9 1.175007 1 0.9 9 crps
#> 10 1.205994 1 0.9 10 crps
#> 11 1.442704 1 0.9 11 crps
#> 12 1.523201 1 0.9 12 crps
#> 13 1.031744 1 0.9 13 crps
#> 14 1.073644 1 0.9 14 crps
#> 15 0.912718 1 0.9 15 crps
#> 16 1.120658 1 0.9 16 crps
#> 17 1.088715 1 0.9 17 crps
#> 18 4.657818 1 0.9 18 crps
#> 19 1.119962 1 0.9 19 crps
#> 20 2.268270 1 0.9 20 crps
#> 21 1.718125 1 0.9 21 crps
#> 22 1.612500 1 0.9 22 crps
#> 23 4.256675 1 0.9 23 crps
#> 24 1.341427 1 0.9 24 crps
#> 25 1.312268 1 0.9 25 crps
#>
#> $all_series
#> score eval_horizon score_type
#> 1 3.752994 1 sum_crps
#> 2 0.965486 2 sum_crps
#> 3 2.011183 3 sum_crps
#> 4 1.488581 4 sum_crps
#> 5 0.915023 5 sum_crps
#> 6 1.382627 6 sum_crps
#> 7 1.966603 7 sum_crps
#> 8 1.628268 8 sum_crps
#> 9 1.175007 9 sum_crps
#> 10 1.205994 10 sum_crps
#> 11 1.442704 11 sum_crps
#> 12 1.523201 12 sum_crps
#> 13 1.031744 13 sum_crps
#> 14 1.073644 14 sum_crps
#> 15 0.912718 15 sum_crps
#> 16 1.120658 16 sum_crps
#> 17 1.088715 17 sum_crps
#> 18 4.657818 18 sum_crps
#> 19 1.119962 19 sum_crps
#> 20 2.268270 20 sum_crps
#> 21 1.718125 21 sum_crps
#> 22 1.612500 22 sum_crps
#> 23 4.256675 23 sum_crps
#> 24 1.341427 24 sum_crps
#> 25 1.312268 25 sum_crps
#>
score(fc2)
#> $series_1
#> score in_interval interval_width eval_horizon score_type
#> 1 4.027405 1 0.9 1 crps
#> 2 1.601258 1 0.9 2 crps
#> 3 3.404619 0 0.9 3 crps
#> 4 0.890614 1 0.9 4 crps
#> 5 2.538261 1 0.9 5 crps
#> 6 2.620900 1 0.9 6 crps
#> 7 1.892433 1 0.9 7 crps
#> 8 0.918860 1 0.9 8 crps
#> 9 1.634557 1 0.9 9 crps
#> 10 1.184265 1 0.9 10 crps
#> 11 1.456347 1 0.9 11 crps
#> 12 1.715809 1 0.9 12 crps
#> 13 1.019106 1 0.9 13 crps
#> 14 0.957008 1 0.9 14 crps
#> 15 1.113928 1 0.9 15 crps
#> 16 1.133647 1 0.9 16 crps
#> 17 1.101088 1 0.9 17 crps
#> 18 2.844725 1 0.9 18 crps
#> 19 1.189586 1 0.9 19 crps
#> 20 3.681478 1 0.9 20 crps
#> 21 2.473191 1 0.9 21 crps
#> 22 1.617496 1 0.9 22 crps
#> 23 4.132401 1 0.9 23 crps
#> 24 1.385082 1 0.9 24 crps
#> 25 1.320426 1 0.9 25 crps
#>
#> $all_series
#> score eval_horizon score_type
#> 1 4.027405 1 sum_crps
#> 2 1.601258 2 sum_crps
#> 3 3.404619 3 sum_crps
#> 4 0.890614 4 sum_crps
#> 5 2.538261 5 sum_crps
#> 6 2.620900 6 sum_crps
#> 7 1.892433 7 sum_crps
#> 8 0.918860 8 sum_crps
#> 9 1.634557 9 sum_crps
#> 10 1.184265 10 sum_crps
#> 11 1.456347 11 sum_crps
#> 12 1.715809 12 sum_crps
#> 13 1.019106 13 sum_crps
#> 14 0.957008 14 sum_crps
#> 15 1.113928 15 sum_crps
#> 16 1.133647 16 sum_crps
#> 17 1.101088 17 sum_crps
#> 18 2.844725 18 sum_crps
#> 19 1.189586 19 sum_crps
#> 20 3.681478 20 sum_crps
#> 21 2.473191 21 sum_crps
#> 22 1.617496 22 sum_crps
#> 23 4.132401 23 sum_crps
#> 24 1.385082 24 sum_crps
#> 25 1.320426 25 sum_crps
#>
score(ensemble_fc)
#> $series_1
#> score in_interval interval_width eval_horizon score_type
#> 1 3.9128976 1 0.9 1 crps
#> 2 1.2309212 1 0.9 2 crps
#> 3 2.5775444 1 0.9 3 crps
#> 4 1.0660615 1 0.9 4 crps
#> 5 1.5577358 1 0.9 5 crps
#> 6 1.9423396 1 0.9 6 crps
#> 7 1.9207983 1 0.9 7 crps
#> 8 1.1652867 1 0.9 8 crps
#> 9 1.3310904 1 0.9 9 crps
#> 10 1.1153715 1 0.9 10 crps
#> 11 1.4436956 1 0.9 11 crps
#> 12 1.5986158 1 0.9 12 crps
#> 13 1.0041339 1 0.9 13 crps
#> 14 0.9987444 1 0.9 14 crps
#> 15 0.9605165 1 0.9 15 crps
#> 16 0.9886714 1 0.9 16 crps
#> 17 0.9830670 1 0.9 17 crps
#> 18 3.7002889 1 0.9 18 crps
#> 19 1.1610788 1 0.9 19 crps
#> 20 2.8856190 1 0.9 20 crps
#> 21 2.0305508 1 0.9 21 crps
#> 22 1.5736270 1 0.9 22 crps
#> 23 4.2574121 1 0.9 23 crps
#> 24 1.3680988 1 0.9 24 crps
#> 25 1.2395085 1 0.9 25 crps
#>
#> $all_series
#> score eval_horizon score_type
#> 1 3.9128976 1 sum_crps
#> 2 1.2309212 2 sum_crps
#> 3 2.5775444 3 sum_crps
#> 4 1.0660615 4 sum_crps
#> 5 1.5577358 5 sum_crps
#> 6 1.9423396 6 sum_crps
#> 7 1.9207983 7 sum_crps
#> 8 1.1652867 8 sum_crps
#> 9 1.3310904 9 sum_crps
#> 10 1.1153715 10 sum_crps
#> 11 1.4436956 11 sum_crps
#> 12 1.5986158 12 sum_crps
#> 13 1.0041339 13 sum_crps
#> 14 0.9987444 14 sum_crps
#> 15 0.9605165 15 sum_crps
#> 16 0.9886714 16 sum_crps
#> 17 0.9830670 17 sum_crps
#> 18 3.7002889 18 sum_crps
#> 19 1.1610788 19 sum_crps
#> 20 2.8856190 20 sum_crps
#> 21 2.0305508 21 sum_crps
#> 22 1.5736270 22 sum_crps
#> 23 4.2574121 23 sum_crps
#> 24 1.3680988 24 sum_crps
#> 25 1.2395085 25 sum_crps
#>
# }