
Latent factor summaries for a fitted mvgam object
Source:R/plot_mvgam_factors.R
plot_mvgam_factors.RdThis function takes a fitted mvgam object and returns plots and
summary statistics for the latent dynamic factors
Arguments
- object
listobject returned frommvgam. Seemvgam()- plot
logicalspecifying whether factors should be plotted
Details
If the model in object was estimated using dynamic factors,
it is possible that not all factors contributed to the estimated trends.
This is due to the regularisation penalty that acts independently on each
factor's Gaussian precision, which will squeeze un-needed factors to a
white noise process (effectively dropping that factor from the model). In
this function, each factor is tested against a null hypothesis of white
noise by calculating the sum of the factor's 2nd derivatives. A factor
that has a larger contribution will have a larger sum due to the weaker
penalty on the factor's precision. If plot == TRUE, the factors
are also plotted.
Examples
# \donttest{
simdat <- sim_mvgam()
mod <- mvgam(
y ~ s(season, bs = 'cc', k = 6),
trend_model = AR(),
use_lv = TRUE,
n_lv = 2,
data = simdat$data_train,
chains = 2,
silent = 2
)
#> Warning in '/tmp/RtmpJcw6T0/model_0f5e123adc47a9208b1c8eaa9e58906b.stan', line 23, column 31: Found
#> int division:
#> n_lv * (n_lv - 1) / 2
#> Values will be rounded towards zero. If rounding is not desired you can
#> write
#> the division as
#> n_lv * (n_lv - 1) / 2.0
#> If rounding is intended please use the integer division operator %/%.
#> Warning in '/tmp/RtmpJcw6T0/model-23ed3f849649.stan', line 23, column 33: Found
#> int division:
#> n_lv * (n_lv - 1) / 2
#> Values will be rounded towards zero. If rounding is not desired you can
#> write
#> the division as
#> n_lv * (n_lv - 1) / 2.0
#> If rounding is intended please use the integer division operator %/%.
plot_mvgam_factors(mod)
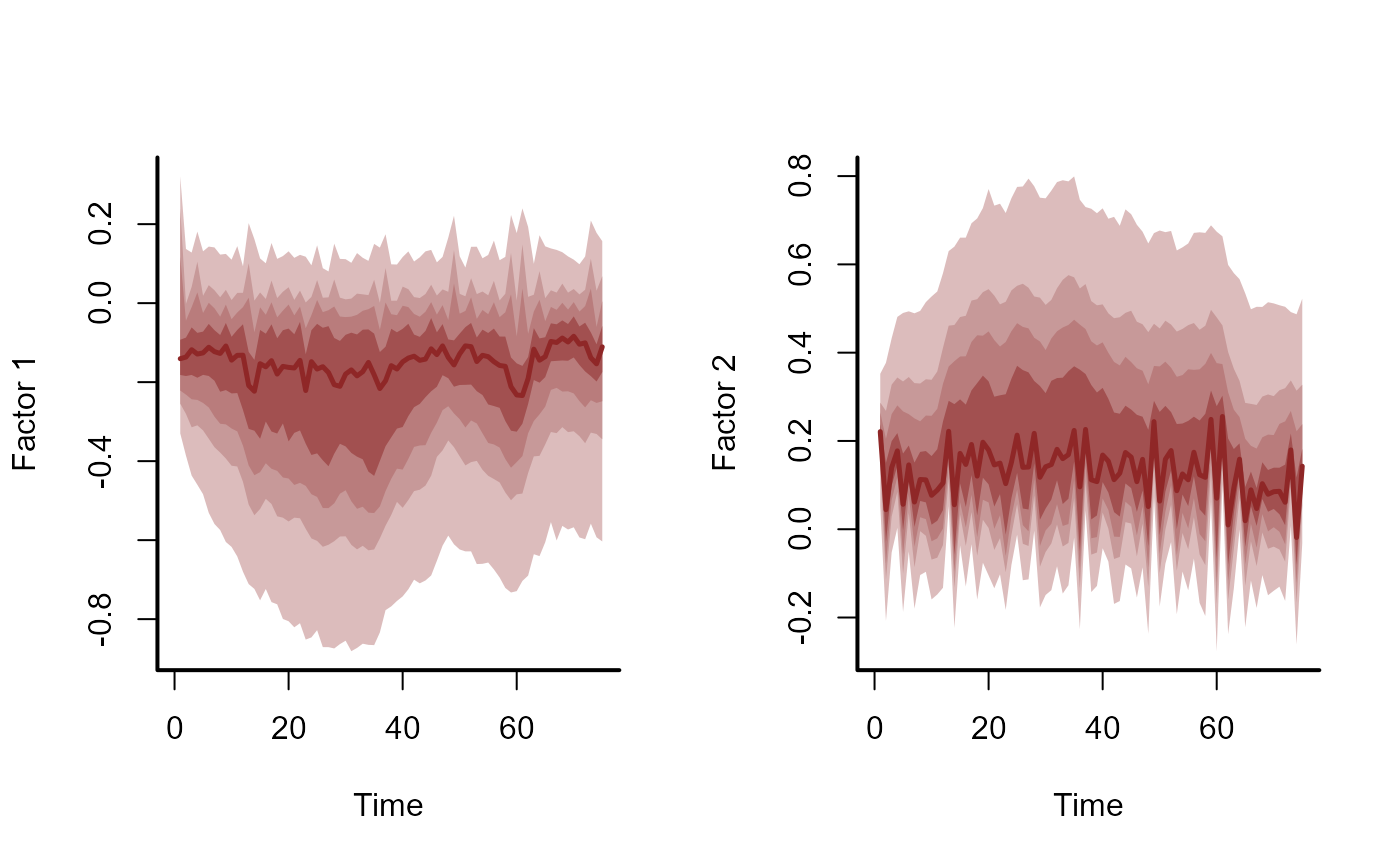 #> # A tibble: 2 × 2
#> Factor Contribution
#> <chr> <dbl>
#> 1 Factor 1 0.528
#> 2 Factor 2 0.472
# }
#> # A tibble: 2 × 2
#> Factor Contribution
#> <chr> <dbl>
#> 1 Factor 1 0.528
#> 2 Factor 2 0.472
# }